


Nächste Seite: Dynamik in der Brown-Gabrielse-Magnetflasche
Aufwärts: Das Størmer-Problem
Vorherige Seite: Diskussion des Størmer-Potentials
Inhalt
Transformation auf Dipolarkoordinaten
Durch die Skalierung haben wir die Hamilton-Funktion vereinfacht, indem
wir ,,unwesentliche`` Zahlenfaktoren eliminiert haben. Leider ist aber
auch die so erhaltene vereinfachte Hamilton-Funktion noch zu
kompliziert, als daß wir sie direkt mit dem Normalformen-Formalismus
analysieren könnten, denn offensichtlich liegt 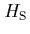 nicht als
Potenzreihe
vor. Eine wesentliche Voraussetzung der Transformation auf Normalform ist
damit nicht erfüllt.
nicht als
Potenzreihe
vor. Eine wesentliche Voraussetzung der Transformation auf Normalform ist
damit nicht erfüllt.
Zur Lösung dieses Problems erinnern wir uns daran, daß wir ohnehin
keine exakte Formel für die Normalform oder für ein drittes (formales)
Integral2.8des Størmer-Problems angeben wollen.
Vielmehr wollen wir diese
Größen
näherungsweise berechnen, und zwar in der Form von
Potenzreihenentwicklungen, die
nach endlich vielen Summanden abgebrochen werden. Es liegt also nahe, in
einem ersten Schritt auch die Hamilton-Funktion des Størmer-Problems
in eine Potenzreihe zu entwickeln und genauso viele Terme dieser
Entwicklung zu berücksichtigen, wie wir für die gewünschte
Genauigkeit des Quasiintegrals benötigen. Wenn wir zum Beispiel das
Quasiintegral bis zur Ordnung 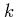 bestimmen wollen, müssen wir zunächst
bestimmen wollen, müssen wir zunächst
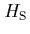 bis zur Ordnung
bis zur Ordnung 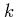 entwickeln.
entwickeln.
Es stellt sich nun vor allem die Frage, welcher Koordinaten man sich für
die Hamilton-Funktion bedienen soll, damit man die Reihenentwicklungen
ab einer gewissen Ordnung abbrechen kann, ohne einen zu großen
Fehler zu erhalten.
So sind zum Beispiel die Zylinderkoordinaten 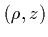 ungeeignet,
denn das Teilchen wird, annähernd einer Feldlinie folgend, relativ stark
sowohl in
ungeeignet,
denn das Teilchen wird, annähernd einer Feldlinie folgend, relativ stark
sowohl in 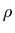 - als auch in
- als auch in 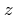 -Richtung oszillieren; dies wird in
Abbildung 2.6 für einen typischen Orbit
veranschaulicht.
-Richtung oszillieren; dies wird in
Abbildung 2.6 für einen typischen Orbit
veranschaulicht.
Statt dessen suchen wir Koordinaten 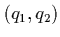 , die der Teilchenbewegung
besser angepaßt sind und sich mit
kleinerer
Amplitude ändern. Wir
haben
schon früher gesehen, daß die Bewegung des Teilchens durch eine
Translation längs einer Feldlinie, überlagert mit der Rotation um diese
Feldlinie herum, beschrieben werden kann. Deshalb verwenden wir die von
Dragt eingeführten orthogonalen Dipolarkoordinaten
(vgl. [Dr65,DrFi79]),
, die der Teilchenbewegung
besser angepaßt sind und sich mit
kleinerer
Amplitude ändern. Wir
haben
schon früher gesehen, daß die Bewegung des Teilchens durch eine
Translation längs einer Feldlinie, überlagert mit der Rotation um diese
Feldlinie herum, beschrieben werden kann. Deshalb verwenden wir die von
Dragt eingeführten orthogonalen Dipolarkoordinaten
(vgl. [Dr65,DrFi79]),
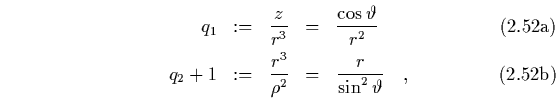
die diesem Bewegungstypus Rechnung tragen, denn Gl. (2.53b)
stimmt mit Gl. (2.44) überein: Die
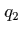 -Koordinatenlinien,
also die Linien mit konstantem
-Koordinatenlinien,
also die Linien mit konstantem 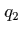 , sind die Dipol-Feldlinien.
, sind die Dipol-Feldlinien.
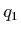 beschreibt die Translation entlang den Feldlinien, während
beschreibt die Translation entlang den Feldlinien, während
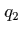 für die Bewegung senkrecht zu ihnen steht.
für die Bewegung senkrecht zu ihnen steht.
Die Transformation auf
Dipolarkoordinaten führt dazu, daß die Dynamik in zwei in erster
Näherung voneinander unabhängige Oszillationen zerlegt wird; die
Oszillation in 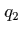 -Richtung (um die Feldlinie herum) ist schneller als
diejenige in
-Richtung (um die Feldlinie herum) ist schneller als
diejenige in 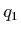 -Richtung (entlang der Feldlinie).
Dabei ist entscheidend, daß diese neuen
Koordinaten um die Null herum oszillieren -- um dies zu erreichen, steht
in Gl. (2.53b) auf der linken Seite
-Richtung (entlang der Feldlinie).
Dabei ist entscheidend, daß diese neuen
Koordinaten um die Null herum oszillieren -- um dies zu erreichen, steht
in Gl. (2.53b) auf der linken Seite 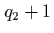 , im
Gegensatz zu Dragts ursprünglicher Definition
, im
Gegensatz zu Dragts ursprünglicher Definition
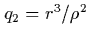 . Wichtig
ist auch, daß
. Wichtig
ist auch, daß 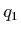 und
und 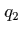 mit nicht zu großer Amplitude oszillieren
-- wie zu fordern ist, wenn eine Reihenentwicklung der
Hamilton-Funktion sinnvoll sein soll. Abbildung 2.7,
mit nicht zu großer Amplitude oszillieren
-- wie zu fordern ist, wenn eine Reihenentwicklung der
Hamilton-Funktion sinnvoll sein soll. Abbildung 2.7,
die den gleichen Orbit wie Abbildung 2.6 in
Dipolarkoordinaten zeigt, veranschaulicht diesen Sachverhalt.
Bei der Transformation von Zylinder- auf Dipolarkoordinaten in Gl. (2.53) handelt es sich nur um eine Punkttransformation
im Konfigurationsraum. Für die vollständige Angabe der entsprechenden
kanonischen Transformation fehlen noch Transformationsformeln für
die zu 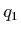 und
und 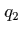 kanonisch-konjugierten Impulse
kanonisch-konjugierten Impulse 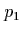 und
und 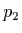 .
Wir benötigen diese Transformationsformeln, um die
Størmersche Hamilton-Funktion in Dipolarkoordinaten formulieren zu
können. Zur Berechnung dieser Formeln suchen wir zunächst eine erzeugende
Funktion vom
.
Wir benötigen diese Transformationsformeln, um die
Størmersche Hamilton-Funktion in Dipolarkoordinaten formulieren zu
können. Zur Berechnung dieser Formeln suchen wir zunächst eine erzeugende
Funktion vom 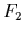 -Typ für die kanonische Transformation:
-Typ für die kanonische Transformation:
Dabei muß für 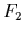 gelten (vgl. zum Beispiel [No90a]):
gelten (vgl. zum Beispiel [No90a]):
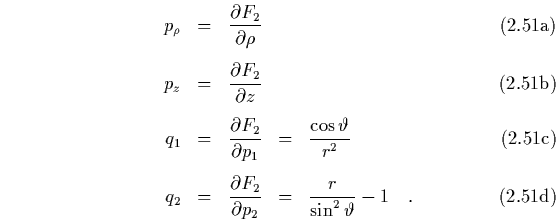
Wir setzen für 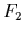 so einfach wie möglich an (und verstehen
so einfach wie möglich an (und verstehen 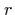 und
und
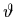 bzw.
bzw. 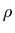 und
und 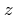 im folgenden als Funktionen von
im folgenden als Funktionen von 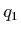 und
und 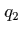 ),
),
wodurch die Gln. (2.54c) und (2.54d) automatisch erfüllt sind.
Die Auswertung der Gln. (2.54a) und (2.54b) ergibt dann
und
Durch Umstellen dieser beiden Gleichungen nach 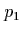 und
und 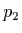 könnte
man explizite Formeln für die zu den Dipolarkoordinaten gehörenden
kanonischen Impulse angeben.
Das ist in unserem Fall aber gar nicht nötig, weil wir lediglich die
Hamilton-Funktion auf die neuen Phasenraumvariablen umschreiben wollen.
Die alten Impulse
könnte
man explizite Formeln für die zu den Dipolarkoordinaten gehörenden
kanonischen Impulse angeben.
Das ist in unserem Fall aber gar nicht nötig, weil wir lediglich die
Hamilton-Funktion auf die neuen Phasenraumvariablen umschreiben wollen.
Die alten Impulse 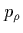 und
und 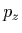 treten in der alten Hamilton-Funktion
nur als Summe ihrer Quadrate auf, so daß wir auch nur diese Summe
als
Funktion von
treten in der alten Hamilton-Funktion
nur als Summe ihrer Quadrate auf, so daß wir auch nur diese Summe
als
Funktion von 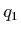 ,
, 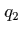 ,
, 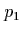 und
und 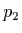 benötigen:
benötigen:
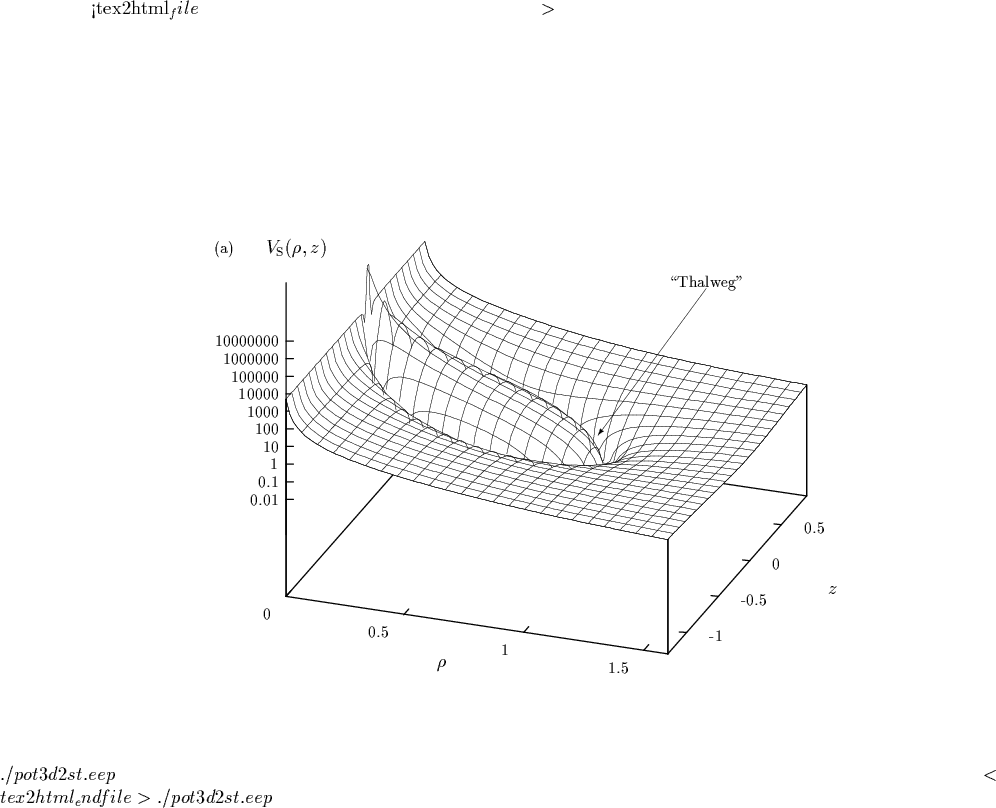
Für das Potential 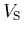 erhalten wir in Dipolarkoordinaten:
erhalten wir in Dipolarkoordinaten:
Damit haben wir das Resultat, daß sich die Størmersche
Hamilton-Funktion (2.46) nach der durch 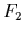 erzeugten kanonischen Transformation auf Dipolarkoordinaten als
erzeugten kanonischen Transformation auf Dipolarkoordinaten als
schreiben läßt mit
In den Gln. (2.59-2.61) stellt 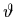 nur
eine abkürzende Schreibweise für
nur
eine abkürzende Schreibweise für
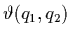 dar, wobei der Zusammenhang zwischen
dar, wobei der Zusammenhang zwischen 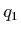 ,
, 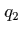 und
und
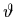 durch Gl. (2.53) gegeben ist.
durch Gl. (2.53) gegeben ist.
Nachdem wir die Hamilton-Funktion
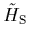 in
Dipolarkoordinaten
formuliert haben, können wir sie jetzt nach den -- als
klein angesehenen --
in
Dipolarkoordinaten
formuliert haben, können wir sie jetzt nach den -- als
klein angesehenen -- 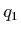 ,
, 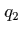 ,
, 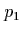 und
und 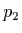 entwickeln.
Zuerst zeigen wir aber noch, daß eine solche Entwicklung in der Tat
sinnvoll ist, weil man durch die Wahl der Energie immer erreichen kann,
daß
entwickeln.
Zuerst zeigen wir aber noch, daß eine solche Entwicklung in der Tat
sinnvoll ist, weil man durch die Wahl der Energie immer erreichen kann,
daß 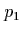 und
und 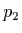 beliebig klein sind und bleiben.
Wir leiten aus Gl. (2.61) die Ungleichungen
beliebig klein sind und bleiben.
Wir leiten aus Gl. (2.61) die Ungleichungen
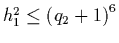 und
und 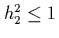 ab und folgern damit
aus Gl. (2.60), daß bei der Energie
ab und folgern damit
aus Gl. (2.60), daß bei der Energie
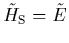 gilt:
gilt:
Hieraus folgt
die Behauptung,
weil 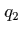 für gebundene Orbits
beschränkt ist, wie wir oben gesehen haben.
Solange man sich also auf solche
Trajektorien
beschränkt, deren Energie
hinreichend
klein ist und die
genügend nahe am ,,Thalweg`` starten,
werden alle vier Phasenraumkoordinaten
für gebundene Orbits
beschränkt ist, wie wir oben gesehen haben.
Solange man sich also auf solche
Trajektorien
beschränkt, deren Energie
hinreichend
klein ist und die
genügend nahe am ,,Thalweg`` starten,
werden alle vier Phasenraumkoordinaten 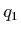 ,
, 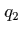 ,
, 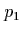 und
und 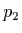 klein bleiben.
klein bleiben.
In Anhang C führen wir die Berechnung der
Potenzreihenentwicklung für
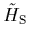 durch. Als Resultat
ergibt sich
die folgende Näherungsformel für die Størmersche Hamilton-Funktion
in Dipolarkoordinaten:
durch. Als Resultat
ergibt sich
die folgende Näherungsformel für die Størmersche Hamilton-Funktion
in Dipolarkoordinaten:
wobei das Symbol
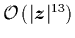 wieder andeuten soll, daß wir
alle Summanden mit einem größeren Totalgrad als 12 in
wieder andeuten soll, daß wir
alle Summanden mit einem größeren Totalgrad als 12 in
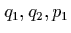 und
und 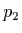 vernachlässigen.
vernachlässigen.
Damit liegt auch die Størmersche Hamilton-Funktion in einer Form
vor, in der sie mit den Mitteln der Normalformentheorie untersucht
werden kann. Wir bemerken, daß
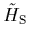 ebensowenig im
Rahmen der
Gustavsonschen Theorie behandelbar ist wie die
Hamilton-Funktionen, die wir in den vorangegangenen Abschnitten
besprochen haben. Erst die Dragt-Finn-Stegemerten-Theorie schafft hier
Abhilfe und ermöglicht die Untersuchung von
ebensowenig im
Rahmen der
Gustavsonschen Theorie behandelbar ist wie die
Hamilton-Funktionen, die wir in den vorangegangenen Abschnitten
besprochen haben. Erst die Dragt-Finn-Stegemerten-Theorie schafft hier
Abhilfe und ermöglicht die Untersuchung von
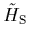 2.9.
2.9.
Das Beispiel des Størmer-Problems zeigt, daß auch Systeme, deren
Hamilton-Funktion nicht in
Form einer Potenzreihe
vorliegt, der Analyse mittels
Normalformentheorie zugänglich sind. Es ist aber offenkundig, daß die
in diesen Fällen notwendige Umformulierung der Hamilton-Funktion große
Schwierigkeiten bereiten kann.
Fußnoten
- ...
Integral2.8
- Die ,,ersten`` beiden Integrale der Bewegung für das
Størmer-Problem sind die Energie und
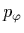 .
.
- ...
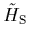 2.9
2.9
- In [CoVl75] wird eine andere Variante der
Untersuchung der Størmer-Hamilton-Funktion
(2.62) mittels Normalformen
angegeben: Um die Behandlung im Rahmen des
Gustavsonschen Formalismus zu ermöglichen, wird die
Hamilton-Funktion in eine andere transformiert, deren
quadratischer Anteil vom Typ (1.61) ist.
Eine solche Transformation der Hamilton-Funktion gelingt aber
bei anderen Systemen im allgemeinen nicht, so daß auch hier
die in jedem Fall durchführbare verallgemeinerte
Normalformentheorie vorzuziehen ist.



Nächste Seite: Dynamik in der Brown-Gabrielse-Magnetflasche
Aufwärts: Das Størmer-Problem
Vorherige Seite: Diskussion des Størmer-Potentials
Inhalt
Martin_Engel
2000-05-25

![]() ungeeignet,
denn das Teilchen wird, annähernd einer Feldlinie folgend, relativ stark
sowohl in
ungeeignet,
denn das Teilchen wird, annähernd einer Feldlinie folgend, relativ stark
sowohl in ![]() - als auch in
- als auch in ![]() -Richtung oszillieren; dies wird in
Abbildung 2.6 für einen typischen Orbit
veranschaulicht.
-Richtung oszillieren; dies wird in
Abbildung 2.6 für einen typischen Orbit
veranschaulicht.
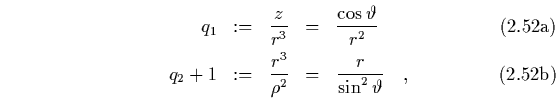
![]() -Richtung (um die Feldlinie herum) ist schneller als
diejenige in
-Richtung (um die Feldlinie herum) ist schneller als
diejenige in ![]() -Richtung (entlang der Feldlinie).
Dabei ist entscheidend, daß diese neuen
Koordinaten um die Null herum oszillieren -- um dies zu erreichen, steht
in Gl. (2.53b) auf der linken Seite
-Richtung (entlang der Feldlinie).
Dabei ist entscheidend, daß diese neuen
Koordinaten um die Null herum oszillieren -- um dies zu erreichen, steht
in Gl. (2.53b) auf der linken Seite ![]() , im
Gegensatz zu Dragts ursprünglicher Definition
, im
Gegensatz zu Dragts ursprünglicher Definition
![]() . Wichtig
ist auch, daß
. Wichtig
ist auch, daß ![]() und
und ![]() mit nicht zu großer Amplitude oszillieren
-- wie zu fordern ist, wenn eine Reihenentwicklung der
Hamilton-Funktion sinnvoll sein soll. Abbildung 2.7,
mit nicht zu großer Amplitude oszillieren
-- wie zu fordern ist, wenn eine Reihenentwicklung der
Hamilton-Funktion sinnvoll sein soll. Abbildung 2.7,
![]() und
und ![]() kanonisch-konjugierten Impulse
kanonisch-konjugierten Impulse ![]() und
und ![]() .
Wir benötigen diese Transformationsformeln, um die
Størmersche Hamilton-Funktion in Dipolarkoordinaten formulieren zu
können. Zur Berechnung dieser Formeln suchen wir zunächst eine erzeugende
Funktion vom
.
Wir benötigen diese Transformationsformeln, um die
Størmersche Hamilton-Funktion in Dipolarkoordinaten formulieren zu
können. Zur Berechnung dieser Formeln suchen wir zunächst eine erzeugende
Funktion vom ![]() -Typ für die kanonische Transformation:
-Typ für die kanonische Transformation:
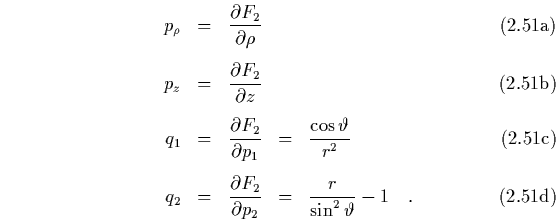
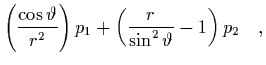
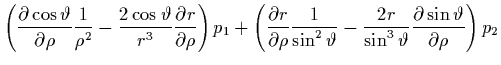
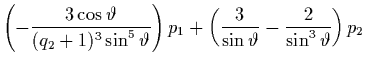
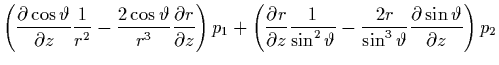
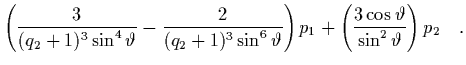
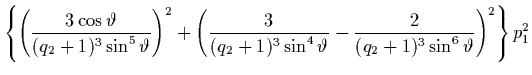
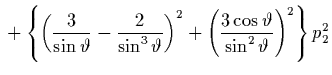
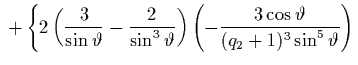
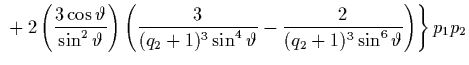
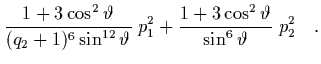
![]() erzeugten kanonischen Transformation auf Dipolarkoordinaten als
erzeugten kanonischen Transformation auf Dipolarkoordinaten als
![]() in
Dipolarkoordinaten
formuliert haben, können wir sie jetzt nach den -- als
klein angesehenen --
in
Dipolarkoordinaten
formuliert haben, können wir sie jetzt nach den -- als
klein angesehenen -- ![]() ,
, ![]() ,
, ![]() und
und ![]() entwickeln.
Zuerst zeigen wir aber noch, daß eine solche Entwicklung in der Tat
sinnvoll ist, weil man durch die Wahl der Energie immer erreichen kann,
daß
entwickeln.
Zuerst zeigen wir aber noch, daß eine solche Entwicklung in der Tat
sinnvoll ist, weil man durch die Wahl der Energie immer erreichen kann,
daß ![]() und
und ![]() beliebig klein sind und bleiben.
Wir leiten aus Gl. (2.61) die Ungleichungen
beliebig klein sind und bleiben.
Wir leiten aus Gl. (2.61) die Ungleichungen
![]() und
und ![]() ab und folgern damit
aus Gl. (2.60), daß bei der Energie
ab und folgern damit
aus Gl. (2.60), daß bei der Energie
![]() gilt:
gilt:
![\begin{eqnarray*}
p_1^2+p_2^2 & \leq & \left\{ \left( \frac{p_1}{h_1} \right)^2...
...6
\\ [0.2cm]
& \leq & 2\tilde{E} \left( q_2+1 \right)^6 \quad.
\end{eqnarray*}](img715.png)
![]() durch. Als Resultat
ergibt sich
die folgende Näherungsformel für die Størmersche Hamilton-Funktion
in Dipolarkoordinaten:
durch. Als Resultat
ergibt sich
die folgende Näherungsformel für die Størmersche Hamilton-Funktion
in Dipolarkoordinaten:
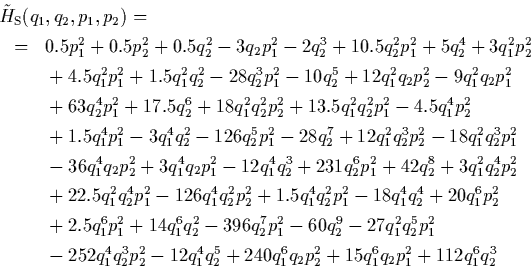
![]() ebensowenig im
Rahmen der
Gustavsonschen Theorie behandelbar ist wie die
Hamilton-Funktionen, die wir in den vorangegangenen Abschnitten
besprochen haben. Erst die Dragt-Finn-Stegemerten-Theorie schafft hier
Abhilfe und ermöglicht die Untersuchung von
ebensowenig im
Rahmen der
Gustavsonschen Theorie behandelbar ist wie die
Hamilton-Funktionen, die wir in den vorangegangenen Abschnitten
besprochen haben. Erst die Dragt-Finn-Stegemerten-Theorie schafft hier
Abhilfe und ermöglicht die Untersuchung von
![]() 2.9.
2.9.