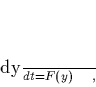


Next: Geometry from an Ideal
Up: Time Series Analysis A
Previous: Contents
Contents
In dynamical systems theory it is a common problem to
analyze a discrete set of observed quantities, a time series.
Consider for example the dynamical
system defined by the differential equation
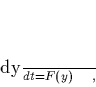 |
(1) |
where
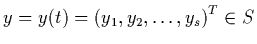 is a vector
representing
the state of the system at time
is a vector
representing
the state of the system at time 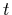 in some
in some 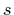 -dimensional phase space
-dimensional phase space
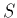 . The vector field
. The vector field 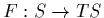 (
(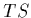 is the tangent space of
is the tangent space of 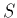 .)
induces the flow
.)
induces the flow
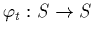 :
:
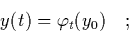 |
(2) |
here, 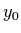 comes from the initial condition
comes from the initial condition 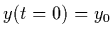 .
Often, when one
analyzes a system, the analytic solution
.
Often, when one
analyzes a system, the analytic solution 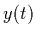 is not known. Instead,
only a time series is available, a series of values of one single
quantity sampled at regular intervals:
is not known. Instead,
only a time series is available, a series of values of one single
quantity sampled at regular intervals:
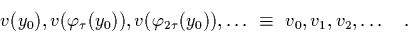 |
(3) |
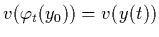 is the value of some observable
is the value of some observable 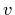 of the
system at time t. The
time interval
of the
system at time t. The
time interval  between two successive measurements of
between two successive measurements of 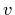 is the
sampling time or delay time.
is the
sampling time or delay time.  need not be fixed; it is
possible to consider the sequence
need not be fixed; it is
possible to consider the sequence
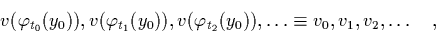 |
(4) |
as well, where the times
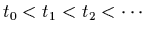 are not equidistant.
One
can get such a time series as the result of an experiment
(where it is often convenient to measure only one single observable)
or from the numerical integration of eq. (1).
It is clear that having only a time series, instead of the complete
solution, is a strong restriction of our knowledge about the system.
Alternatively, one might have a discrete dynamical system, defined
by the mapping
are not equidistant.
One
can get such a time series as the result of an experiment
(where it is often convenient to measure only one single observable)
or from the numerical integration of eq. (1).
It is clear that having only a time series, instead of the complete
solution, is a strong restriction of our knowledge about the system.
Alternatively, one might have a discrete dynamical system, defined
by the mapping
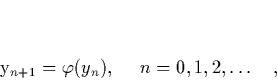 |
(5) |
where
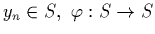 , and get the time series
, and get the time series
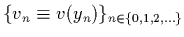 .
As the system evolves, the trajectory in the phase space
.
As the system evolves, the trajectory in the phase space 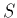 approaches an
attractor1
approaches an
attractor1 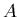 which lies within some submanifold
which lies within some submanifold 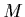 of
of 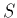 :
:
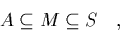 |
(6) |
where
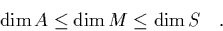 |
(7) |
The general aim of the analysis of the time series is to describe the
behaviour of the system on this attractor  . One would like to
reconstruct a geometric picture of
. One would like to
reconstruct a geometric picture of  in phase space. Also one is
interested in characterizing
in phase space. Also one is
interested in characterizing 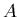 by calculating its
Hausdorff-Besikovich (or fractal) dimension,
information dimension, correlation dimension, Lyapunov exponents, etc.
The problems one encounters when computing these quantities from a
time series will be discussed in this essay.
In section 2, we will show how an embedding trick can be used to get a
simple technique of reconstruction of phase space pictures.
Section 3 deals with the application of this technique. In particular,
we will present several strategies how to choose some of the important
parameters of the reconstruction. Additionally, we will consider the
problems arising from noisy data, and we will discuss the requirements
the data (i.e. the time series) has to fulfill to allow for reasonable
results. The important news is that, in fact, it is possible to get those
reasonable results, despite of the very restricted form of the data.
by calculating its
Hausdorff-Besikovich (or fractal) dimension,
information dimension, correlation dimension, Lyapunov exponents, etc.
The problems one encounters when computing these quantities from a
time series will be discussed in this essay.
In section 2, we will show how an embedding trick can be used to get a
simple technique of reconstruction of phase space pictures.
Section 3 deals with the application of this technique. In particular,
we will present several strategies how to choose some of the important
parameters of the reconstruction. Additionally, we will consider the
problems arising from noisy data, and we will discuss the requirements
the data (i.e. the time series) has to fulfill to allow for reasonable
results. The important news is that, in fact, it is possible to get those
reasonable results, despite of the very restricted form of the data.
Footnotes
- ...attractor1
-
We assume that our dynamical system is dissipative, i.e. the phase
flow
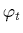 (or the map
(or the map 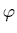 , respectively) contracts volume in
(some part of) the phase space. Otherwise the discussion of attractors
would not be very meaningful.
, respectively) contracts volume in
(some part of) the phase space. Otherwise the discussion of attractors
would not be very meaningful.



Next: Geometry from an Ideal
Up: Time Series Analysis A
Previous: Contents
Contents
Martin_Engel
2000-05-25