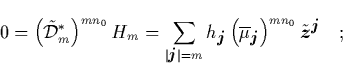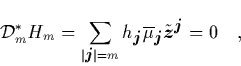


Next: Normalizing a magnetic bottle
Up: Normal forms
Previous: The generalized normal form
Contents
Quasi-integrals of motion
By construction, for a Hamiltonian in BGNF  is a formal integral of
motion (see section 2.1). We now show how to find
an analogous formal integral for a Hamiltonian in generalized normal form.
Our results are similar to the findings of Meyer and Hall
[19], but the proof differs in some details. We have tried
to make the exposition as transparent as possible by focusing on just
those aspects that are essential
for the reasoning.
is a formal integral of
motion (see section 2.1). We now show how to find
an analogous formal integral for a Hamiltonian in generalized normal form.
Our results are similar to the findings of Meyer and Hall
[19], but the proof differs in some details. We have tried
to make the exposition as transparent as possible by focusing on just
those aspects that are essential
for the reasoning.
We write
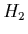 as
as
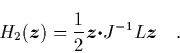 |
(16) |
and
decompose 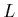 by means of the Jordan-Chevalley decomposition
[25] into its diagonalizable and nilpotent parts
by means of the Jordan-Chevalley decomposition
[25] into its diagonalizable and nilpotent parts 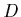 and
and
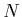 :
:
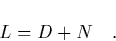 |
(17) |
Existence
and uniqueness of this decomposition are assured by the Jordan normal form
theorem for matrices.
Define the diagonalizable component
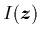 and the
nilpotent component
and the
nilpotent component
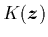 of
of
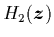 by
by
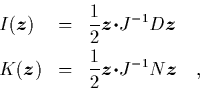 |
(18) |
such that
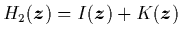 .
We are now in the position to prove the main
.
We are now in the position to prove the main
Theorem:
For a Hamiltonian
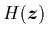 in generalized normal form the
diagonalizable part
in generalized normal form the
diagonalizable part
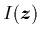 of
of
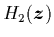 is a formal integral
of motion.
is a formal integral
of motion.
For the proof we must show that the Poisson bracket of 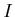 with
with 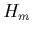 vanishes for all
vanishes for all 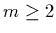 . We start with
. We start with 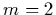 and then proceed to the
case
and then proceed to the
case 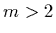 .
.
By virtue of Jacobi's identity for the Poisson bracket we have
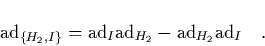 |
(19) |
This expression is zero if
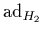 and
and
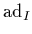 commute.
In order to show that the latter is the case we first remark that the
matrices
commute.
In order to show that the latter is the case we first remark that the
matrices 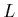 ,
, 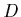 and
and 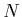 are infinitesimally symplectic
[26], i.e. they satisfy
are infinitesimally symplectic
[26], i.e. they satisfy 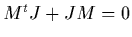 (for
(for 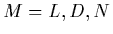 ).
Direct computation shows that for an infinitesimally symplectic
matrix
).
Direct computation shows that for an infinitesimally symplectic
matrix 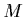 the Lie operator adjoint to the quadratic polynomial
the Lie operator adjoint to the quadratic polynomial
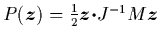 can be written as
can be written as
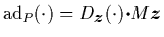 .
Thus we have for the Lie operators
.
Thus we have for the Lie operators 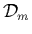 and
and 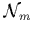 adjoint to
adjoint to 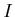 and
and 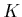 :
:
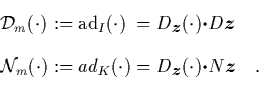 |
(20) |
It is one of the key advantages of this formulation of the theory that we
can characterize all the important operators 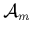 ,
, 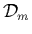 and
and 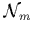 which operate in a space of the high dimension
which operate in a space of the high dimension
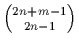 by matrices of the considerably smaller dimension
by matrices of the considerably smaller dimension
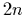 :
: 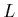 ,
, 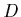 and
and 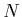 .
.
We now show that for two commuting matrices 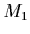 ,
, 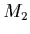 the corresponding
Lie operators
the corresponding
Lie operators
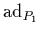 ,
,
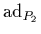 (defined as above)
commute as well:
(defined as above)
commute as well:
Because
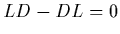 this implies that the right hand side of (27)
is zero, and thus
this implies that the right hand side of (27)
is zero, and thus
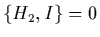 .
.
For 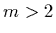 we proceed in the following way: We show that diagonalizability
and nilpotence of the matrices
we proceed in the following way: We show that diagonalizability
and nilpotence of the matrices 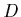 and
and 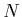 carry over to the corresponding
Lie operators
carry over to the corresponding
Lie operators 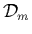 and
and 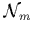 ; these properties then imply that
the null spaces of
; these properties then imply that
the null spaces of 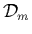 and
and 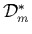 coincide and that
coincide and that
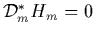 , which in turn means
, which in turn means
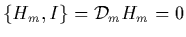 .
.
Consider a unitary matrix 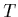 that transforms
that transforms 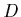 into the diagonal matrix
into the diagonal matrix
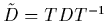 .
Inserting twice the identity
.
Inserting twice the identity 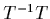 into the expression for
into the expression for 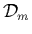 we get
we get
With
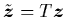 ,
and denoting
,
and denoting 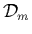 in the new coordinates
in the new coordinates
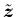 by
by
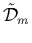 , we obtain
, we obtain
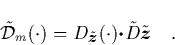 |
(22) |
Application of this transformed operator to any of the basis monomials
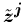 of
of 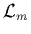 yields, because
yields, because 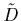 is
diagonal, an eigenvalue equation with the eigenfunction
is
diagonal, an eigenvalue equation with the eigenfunction
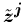 and a certain eigenvalue
and a certain eigenvalue
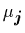 --
thus diagonalizability of
--
thus diagonalizability of 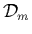 is shown.
is shown.
Now consider any 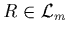 .
.
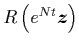 is a
polynomial in
is a
polynomial in 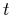 of degree less than or equal to
of degree less than or equal to 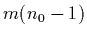 ,
since by nilpotence there is some
,
since by nilpotence there is some 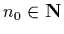 such that
such that 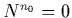 .
This polynomial is related to
.
This polynomial is related to 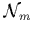 in the following way:
in the following way:
Iterating this expression and evaluating for  we get
we get
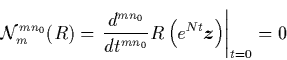 |
(23) |
which implies nilpotence of 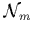 , because (31)
holds for all
, because (31)
holds for all 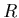 .
.
Identity of the null spaces of 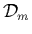 and
and 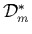 is a direct
implication of diagonalizability: Application of the diagonalized operator
is a direct
implication of diagonalizability: Application of the diagonalized operator
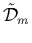 (cf. (30)) yields
(cf. (30)) yields
So the eigenspaces corresponding to the eigenvalue 0 of 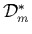 and
and
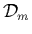 are identical.
are identical.
Finally, we determine how 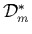 acts on polynomials in
acts on polynomials in 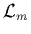 .
Notice that
.
Notice that 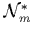 is nilpotent, because its adjoint is.
With
is nilpotent, because its adjoint is.
With
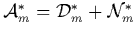 we obtain for any
we obtain for any 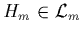 :
:
because 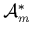 and
and 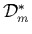 commute (since the corresponding matrices
commute (since the corresponding matrices
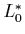 and
and 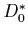 commute; cf. (29)).
commute; cf. (29)).
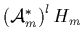 is zero for
is zero for 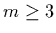 and
and 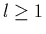 because
because
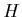 is in generalized normal form. From this it follows for
is in generalized normal form. From this it follows for
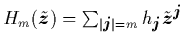 that
that
here, for the sake of notational convenience, we have again turned to
the coordinates
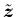 as defined above.
Linear independence of the basis monomials
as defined above.
Linear independence of the basis monomials
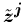 then gives the result
then gives the result
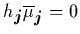 and thus
and thus
and we have proven the theorem.



Next: Normalizing a magnetic bottle
Up: Normal forms
Previous: The generalized normal form
Contents
Martin_Engel
2000-05-25
![]() is a formal integral of
motion (see section 2.1). We now show how to find
an analogous formal integral for a Hamiltonian in generalized normal form.
Our results are similar to the findings of Meyer and Hall
[19], but the proof differs in some details. We have tried
to make the exposition as transparent as possible by focusing on just
those aspects that are essential
for the reasoning.
is a formal integral of
motion (see section 2.1). We now show how to find
an analogous formal integral for a Hamiltonian in generalized normal form.
Our results are similar to the findings of Meyer and Hall
[19], but the proof differs in some details. We have tried
to make the exposition as transparent as possible by focusing on just
those aspects that are essential
for the reasoning.
![]() as
as
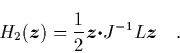
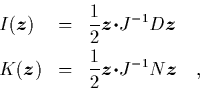
![]() in generalized normal form the
diagonalizable part
in generalized normal form the
diagonalizable part
![]() of
of
![]() is a formal integral
of motion.
is a formal integral
of motion.
![]() with
with ![]() vanishes for all
vanishes for all ![]() . We start with
. We start with ![]() and then proceed to the
case
and then proceed to the
case ![]() .
.
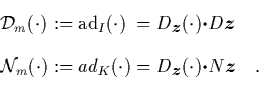
![]() ,
, ![]() the corresponding
Lie operators
the corresponding
Lie operators
![]() ,
,
![]() (defined as above)
commute as well:
(defined as above)
commute as well:
![]() we proceed in the following way: We show that diagonalizability
and nilpotence of the matrices
we proceed in the following way: We show that diagonalizability
and nilpotence of the matrices ![]() and
and ![]() carry over to the corresponding
Lie operators
carry over to the corresponding
Lie operators ![]() and
and ![]() ; these properties then imply that
the null spaces of
; these properties then imply that
the null spaces of ![]() and
and ![]() coincide and that
coincide and that
![]() , which in turn means
, which in turn means
![]() .
.
![]() that transforms
that transforms ![]() into the diagonal matrix
into the diagonal matrix
![]() .
Inserting twice the identity
.
Inserting twice the identity ![]() into the expression for
into the expression for ![]() we get
we get
![]() .
.
![]() is a
polynomial in
is a
polynomial in ![]() of degree less than or equal to
of degree less than or equal to ![]() ,
since by nilpotence there is some
,
since by nilpotence there is some ![]() such that
such that ![]() .
This polynomial is related to
.
This polynomial is related to ![]() in the following way:
in the following way:
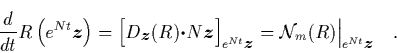
![]() and
and ![]() is a direct
implication of diagonalizability: Application of the diagonalized operator
is a direct
implication of diagonalizability: Application of the diagonalized operator
![]() (cf. (30)) yields
(cf. (30)) yields
![]() acts on polynomials in
acts on polynomials in ![]() .
Notice that
.
Notice that ![]() is nilpotent, because its adjoint is.
With
is nilpotent, because its adjoint is.
With
![]() we obtain for any
we obtain for any ![]() :
:
![\begin{eqnarray*}
\quad
0 & = & ({\cal N}_m^*)^{mn_0} H_m \\ [0.2cm]
& = & ({...
...}_m^* \right)^{mn_0-l}
\left( {\cal A}_m^* \right)^l H_m \quad,
\end{eqnarray*}](img167.png)