Local and global analysis of the quasi-integral

The characteristic property of an integral of motion is its constancy along trajectories in phase space. As mentioned earlier, one cannot expect this behaviour for a formal integral of a nonintegrable system like the magnetic bottle discussed here. But in line with reference [28] (and many others) we still expect convergence of $I({\mbox{\protect\boldmath$z$}})$ in regular regions of phase space.

Let us define the quasi-integral $I^{(m)}({\mbox{\protect\boldmath$z$}})$ of order $m$ as that approximation to $I({\mbox{\protect\boldmath$z$}})$ that contains only monomials of degree $m$ and less:

$$\quad I^{(m)}({\mbox{\protect\boldmath$z$}}) = I({\mbox{\pr... ...t(\vert{\mbox{\protect\boldmath$z$}}\vert^{m+1}\right)} \quad.$$

In order to check the convergence of $I^{(m)}$ as a function of $m$, we choose a point ${\mbox{\protect\boldmath$s$}}\in\Sigma_E$ of the Poincaré surface of section and evaluate the quasi-integral for ${\mbox{\protect\boldmath$z$}}(t)=\Phi_t({\mbox{\protect\boldmath$s$}})$ with $\Phi_t({\mbox{\protect\boldmath$s$}})$ being the phase flow of the system (33):

$$\quad I^{(m)}(t;{\mbox{\protect\boldmath$s$}}) = I^{(m)}\left(\Phi_t({\mbox{\protect\boldmath$s$}})\right) \quad.$$

Figure 4 demonstrates that it depends both on the energy (tantamount to the ``degree of chaoticity'' of the system) and on the starting point ${\mbox{\protect\boldmath$s$}}$ whether convergence of the quasi-integral $I^{(m)}(t;{\mbox{\protect\boldmath$s$}})$ is observed or not. At the low energy $E=0.01$ most ${\mbox{\protect\boldmath$s$}}$ yield fast convergence (figure 4a). At the energy $E=0.2$ divergence occurs almost everywhere, but it is typical that for the first few values of $m$ one has ``pseudo-convergence'' before the expected divergence takes over (figure 4b).

The above analysis is local in the sense that one has to specify a single point ${\mbox{\protect\boldmath$s$}}$ for which $I^{(m)}(t;{\mbox{\protect\boldmath$s$}})$ ist evaluated. We now turn to a kind of global analysis and show how to obtain a qualitative picture of the convergence properties of $I({\mbox{\protect\boldmath$z$}})$ in a larger region of phase space.

In order to have a (though somewhat strong) criterion for convergence we say that $I^{(m)}(t;{\mbox{\protect\boldmath$s$}})$ is convergent at ${\mbox{\protect\boldmath$s$}}$ if

$$\quad \left\vert \overline{I^{(m+2)}}({\mbox{\protect\bold... ...$}}) \right\vert \quad \mbox{for} \quad m=4,6,8,10,12 \quad.$$ (29)

Here $\overline{I^{(m)}}({\mbox{\protect\boldmath$s$}}) = \lim_{T\to\infty} \frac{1}{T} \int_0^T I^{(m)}(t;{\mbox{\protect\boldmath$s$}})$ is the time average of the quasi-integral for a trajectory starting at ${\mbox{\protect\boldmath$s$}}$. It would be highly desirable to extend the definition to higher orders $m$ of the quasi-integral, but this is limited by the great computational effort needed for this task. Our definition is similar to the one suggested in [28], but we find it appropriate to caculate averages over whole trajectories rather than considering just the behaviour at the point ${\mbox{\protect\boldmath$s$}}$.

The next step is to define a convergence function $C({\mbox{\protect\boldmath$s$}})$ by setting

$$% latex2html id marker 809C({\mbox{\protect\boldmath$s$}}... ...y} \; \mbox{in the sense of (\ref{ConvergenceDef})} \right..$$ (30)

Though being quite coarse-grained (since it takes into account only the first few approximants of the formal integral) $C({\mbox{\protect\boldmath$s$}})$ allows to estimate the convergence properties reasonably well.

In figure 5 we present a convergence plot for the magnetic bottle (33) at the energy $E=0.2$. This picture should be compared with figure 3b. On a $200 \times 200$ grid we have marked with black all points where $C({\mbox{\protect\boldmath$s$}})=1$ indicates convergence of the quasi-integral. It is interesting to see that although the condition (39) is quite strong there are large convergent regions in $\Sigma_E$. Many of the details of the Poincaré plot 3b show up in the convergence plot as well. As expected, convergence is most frequent in the centre of the picture. Furthermore, the hyperbolic periodic points of the two dominant Birkhoff chains (of period four and six, respectively) in figure 3b are clearly represented in figure 5 by clouds of black marks. This is surprising, because in the neighbourhoods of these hyperbolic points one would expect distinct divergent behaviour, caused by the chaotic dynamics in a heteroclinic tangle scenario.

As an aside we remark that the convergence of the quasi-integral for the magnetic bottle considered here is worse than the convergence for the Hénon-Heiles system discussed in [28]. This seems to be due to the fact that for the latter system the accessible region of phase space is bounded, whereas for the magnetic bottle the dynamical region extends infinitely along the $z$-axis.

In order to get refined information about the convergence properties of the $I^{(m)}({\mbox{\protect\boldmath$z$}})$ as a function of $m$ we now modify the rule for marking points in the convergence plot. As a measure for the deviation of $I^{(m)}({\mbox{\protect\boldmath$z$}})$ from its mean value we calculate the standard deviation

$$\sigma^{(m)}({\mbox{\protect\boldmath$s$}}) = \sqrt{ \lim_... ...ne{I^{(m)}}({\mbox{\protect\boldmath$s$}}) \right)^2 \, dt }$$

and for normalization (and for comparability of results that belong to different ${\mbox{\protect\boldmath$s$}}$ and thus to different mean values of the quasi-integral) we divide by $\left\vert \overline{I^{(m)}}({\mbox{\protect\boldmath$s$}}) \right\vert$:

$$\quad \eta^{(m)}({\mbox{\protect\boldmath$s$}}) := \frac{ ... ...e{I^{(m)}}({\mbox{\protect\boldmath$s$}}) \right\vert} \quad.$$

This quantity will play a key role in the following. We can take

$$\eta^{(m)}({\mbox{\protect\boldmath$s$}}) < \eta^{(m-2)}({\... ...otect\boldmath$s$}}) \quad \mbox{for} \quad m=4,6,8,\ldots,14$$ (31)

as new necessary criterion for convergence. This criterion is similar, but not equal to (39). With (41) one can say more about the divergent quasi-integrals: For each of them there is an $m_0({\mbox{\protect\boldmath$s$}})$ such that $\eta^{(m_0)}({\mbox{\protect\boldmath$s$}}) \leq \eta^{(m)}({\mbox{\protect\boldmath$s$}})$ for all $m\neq m_0$. A convergent (in the sense of (41)) quasi-integral is characterized by $m_0({\mbox{\protect\boldmath$s$}})=14$ (the highest order of approximation). If divergence occurs from the beginning, i.e. if the deviation of the quasi-integral from its mean value grows for all available $m$, then we have $m_0({\mbox{\protect\boldmath$s$}})=2$. Intermediate values are possible as well. A typical situation (with $m_0=8$) is shown in figure 6.

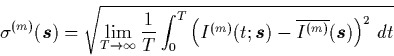
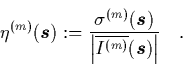
Again we can mark the points of the surface of section of the magnetic bottle, this time according to the value of $m_0({\mbox{\protect\boldmath$s$}})$. The result can be seen in figure 7 which is to be compared with the Poincaré plots of figure 3. The dark regions correspond to larger values of $m_0({\mbox{\protect\boldmath$s$}})$, thus indicating -- cum grano salis -- convergence, while points in the light grey or white areas have small $m_0({\mbox{\protect\boldmath$s$}})$, which means that $\eta^{(m)}({\mbox{\protect\boldmath$s$}})$ increases quite from the beginning. The Poincaré plot 3a at a very low energy shows regular motion, and figure 7a accordingly indicates convergence in large regions of $\Sigma_E$. The light grey spots in the centre of the figure must not be mistaken as indicating divergent behaviour. On the contrary, convergence is excellent around the origin, such that very small values of $\eta^{(m)}({\mbox{\protect\boldmath$s$}})$ are being compared, and values of $m_0({\mbox{\protect\boldmath$s$}})$ larger than two are due to the limited accuracy of the numerical calculation and round-off. Convergence deteriorates with increasing $E$ (und thus increasing chaoticity) as the comparison of figures 3b,c and 7b,c shows. Especially figure 7b reproduces the content of the Kaluza-Robnik-type picture 5 very well and even adds on much more information about the convergent regions. We conclude that the $m_0({\mbox{\protect\boldmath$s$}})$-plots are considerably better suited than the $C({\mbox{\protect\boldmath$s$}})$-plots for the analysis of the convergence properties of the quasi-integral.

It is important to keep in mind that we are using quite a special definition of ``convergence'' here. While this is useful for the present discussion, comparison with rigorous theoretical results about the divergence mechanism [31,32] is delicate. Generally, (pseudo-) convergence (in the usual sense) is expected within a disc, which is compatible with figures 5 and 7a. But figure 7b seems to indicate that convergence has spread into the region between the island chains of period four and six, at variance to the theoretical prediction. The reason being that $m_0({\mbox{\protect\boldmath$s$}})=2$ or 4 reflects only the behaviour for the first few orders $m$ and is no direct indicator for true convergence. So the values of $m_0({\mbox{\protect\boldmath$s$}})$ can be taken only as a vague phenomenological hint towards true convergence or divergence.

Figure 7b already reproduces reasonably well the features of the corresponding Poincaré plot, but only in regions not too far away from the origin. In an attempt to enlarge the region that is accessible for the analysis we make the following exponential ansatz for the normalized standard deviations as functions of $m$:

$$\quad\eta^{(m)}({\mbox{\protect\boldmath$s$}}) \approx a({\... ...({\mbox{\protect\footnotesize\protect\boldmath$s$}}) m} \quad,$$ (32)

with $a({\mbox{\protect\boldmath$s$}})$ and $\alpha({\mbox{\protect\boldmath$s$}})$ to be determined. Here, one is especially interested in the speed of convergence/divergence that is expressed by $\alpha({\mbox{\protect\boldmath$s$}})$. For a justification of the approximation (42), we have considered some typical graphs of $\eta^{(m)}({\mbox{\protect\boldmath$s$}})$ in figure 8 and determined (with a least squares method) the corresponding $a({\mbox{\protect\boldmath$s$}})$ and $\alpha({\mbox{\protect\boldmath$s$}})$. As can be concluded from figures 8a and b, often the approximation (42) seems to work reasonably well. Figure 8c shows a case where a transition from convergence to divergence occurs. Taking into account situations like this, we have to decided to rely only on the $\eta^{(m)}({\mbox{\protect\boldmath$s$}})$ with $m=8,10,12,14$ for the calculation of $\alpha({\mbox{\protect\boldmath$s$}})$, because we are mainly interested in the convergence properties for larger values of $m$. With this convention even a behaviour as in figure 8c can be handled reasonably.

It is one of the advantages of the $\alpha({\mbox{\protect\boldmath$s$}})$-method that one obtains a continuous spectrum of values of $\alpha({\mbox{\protect\boldmath$s$}})$, as opposed to the discrete spectra of $C({\mbox{\protect\boldmath$s$}})$ and $m_0({\mbox{\protect\boldmath$s$}})$. This becomes apparent in figure 9 where we show again $\Sigma_{0.2}$, now shaded according to $\alpha({\mbox{\protect\boldmath$s$}})$. The lighter the grey, the larger $\alpha({\mbox{\protect\boldmath$s$}})$ and thus the faster the divergence of the quasi-integral. The central portion of the picture is similar to the one of figure 7b, but now the outer regions show some structure, too. Comparing with the corresponding Poincaré plot (figure 3b) one sees that the $\alpha({\mbox{\protect\boldmath$s$}})$-plot clearly marks the third and fourth largest Birkhoff chains as well. And even more structure can be detected by more careful analysis of the picture. So the ansatz (42) seems to be justified.