The model system

We consider a ``magnetic bottle'' which is made up of a homogeneous magnetic (dipole) field with a superimposed octupole contribution. In cylindrical coordinates we have:

$$\quad {\mbox{\protect\boldmath$B$}}(\rho,z) := B_0{\mbox{\... ...2}\rho^2\right){\mbox{\protect\boldmath$e$}}_z \right] \quad.$$ (24)

A configuration of this kind was used, for example, for very accurate measurements of the $g$-factor of the electron [27]. Figure 1 shows the field lines of ${\mbox{\protect\boldmath$B$}}(\rho,z)$ and motivates the term ``bottle'': At least in the vicinity of the $z$-axis, the motion of a charged particle in this type of magnetic field consists of a cyclotron oscillation about the field lines, superimposed to a vertical oscillation along these lines. Since the field lines converge towards the $z$-axis for larger values of $\vert z\vert$ the particle will be reflected at some stage (if it does not move exactly on the $z$-axis all the time), and the resulting motion is bound. So ${\mbox{\protect\boldmath$B$}}$ indeed functions as a bottle for charged particles. (This analysis can easily be made rigorous.)

We restrict ourselves to the case $p_\varphi=0$, such that a particle in the bottle does not encircle the $z$-axis but continually passes through it. After suitable scaling we arrive (for $B_0B_2>0$) at the Hamiltonian

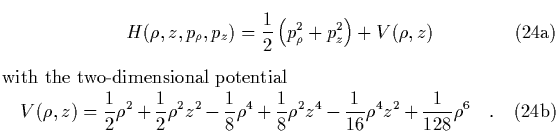
$H$ describes a system with two degrees of freedom, one of which ($\rho$) corresponds, in lowest order approximation, to a harmonically bound motion while the dynamics along the $z$-axis is free in the same approximation. Note that this Hamiltonian cannot be dealt with by the BGNF theory.

In what follows, we do not restrict $\rho$ to positive values but allow for negative values as well. This makes it possible to treat $\rho$ and $z$ simply as cartesian coordinates in two dimensions. An example for the dynamics of our model system, obtained by numerical integration, is shown in figure 2. Similarly, we have numerically calculated Poincaré plots for several energies $E$. To this end we have defined Poincaré surfaces of section $\Sigma_E$ by setting $\rho=0$,

$$\quad \Sigma_E := \left\{ (0,z,p_\rho,p_z)^T\in{\bf R}^4 \... ...=\sqrt{2E-p_z^2}; \; \vert p_z\vert<\sqrt{2E} \right\} \quad,$$

and obtained the corresponding Poincaré plot by recording the points $(z,p_z)$ where the trajectory passes through $\Sigma_E$ with positive momentum $p_\rho$. See figure 3. The system exhibits a typical KAM scenario when the control parameter $E$ is increased; at low energies the system is nearly integrable, whereas at higher energies invariant tori break up and the chaotic region of phase space becomes increasingly large.

It is important to realize that for this system a global second integral of motion (the first being the Hamiltonian itself) cannot exist, because the existence of such an integral would render the system integrable. This would be incompatible with the non-integrability demonstrated by the Poincaré plots. Still, the preceding section shows how to construct a formal invariant. The resolution of this ostensible contradiction is that one expects the formal integral to approximate the local exact integrals of motion in the regular regime (where the KAM tori dominate) whereas in the stochastic regions the formal integral is expected to diverge. See [28] for a discussion of these convergence properties.

Rather than discussing just the Hamiltonian (33) we will study the normalization process for the more general class of magnetic bottle Hamiltonians which are defined by their quadratic contribution:

$$\quad H_2({\mbox{\protect\boldmath$z$}}) = \sum_{\nu=1}^l ... ...\frac{\omega_\nu}{2} \left(z_\nu^2+z_{n+\nu}^2\right) \quad.$$ (24)

With $l=1$, $n=2$, $z_1=z$, $z_2=\rho$ and $\omega_2=1$ we can write the $H_2$ of (33) in the form (34).

Transformation of the corresponding Hamiltonian matrix $L=J\mbox{Hess}(H_2)$ into Jordan normal form yields

$$\quad \tilde{L} = \mbox{diag} \Bigg( \underbrace{\left(\... ...dots,i\omega_n,-i\omega_{l+1},\ldots,-i\omega_n \Bigg) \quad.$$ (25)

Obviously the frequencies $\omega_\nu$ mark the diagonalizable component of $\tilde{L}$ (and therefore of $L$), such that we obtain

$$\quad I_{\rm NF}({\mbox{\protect\boldmath$z$}}) = \sum_{\n... ...frac{\omega_\nu}{2} \left( z_\nu^2+z_{n+\nu}^2 \right) \quad,$$ (26)

which is a formal integral of motion if $H({\mbox{\protect\boldmath$z$}})$ is in generalized normal form. This result was already stated in [17], but here it could be derived with much more ease of computation. For the specific case of (33) we have

$$\quad I_{\rm NF}(\rho,z,p_\rho,p_z) = \frac{1}{2} \left( \rho^2+p_\rho^2 \right) \quad.$$ (27)

The stage is set for application of the normalization process as described in section 2. In the appendix we explain in some detail how the effort needed to normalize magnetic bottle Hamiltonians can be reduced considerably. As the result of these considerations we have obtained the formal integral of the magnetic bottle (33) up to and including the 14th order. The first few terms are

$$I(\rho,z,p_\rho,p_z) = %%***************************************************** 0.5 p_\rho^2 +0.5 \rho^2 +0.046875 p_\rho^4 +0.125 p_z^2 p_\rho^2$$

$${} +0.09375 \rho^2 p_\rho^2 -0.125 \rho^2 p_z^2 -0.078125 \rho^4 +0.5 z \rho p_z p_\rho$$

$${} -0.25 z^2 p_\rho^2 +0.25 z^2 \rho^2 + {{\cal O}\left(\vert{\mbox{\protect\boldmath$z$}}\vert^{6}\right)} \quad.$$ (28)

A complete list of all the 415 summands up to order 14 is available on request from the authors. Note that $I({\mbox{\protect\boldmath$z$}})$ contains only monomials of even order, because the same is true for the original Hamiltonian (33).

It is important to note the difference between the representations (37) and (38) of the integral of motion. The first formula applies if the Hamiltonian is already in generalized normal form, while the second holds for the non-normalized Hamiltonian (33) in the original coordinates and is obtained from (37) by inverting the normalizing Lie transformations.

To our knowledge, there is only one other example in the literature where normalization for a full Hamiltonian has been carried out up to such a high order [28,29]. (Discrete mappings, on the other hand, have been normalized up to order 100 and beyond; cf. [30].) One has to realize, though, that the Hénon-Heiles Hamiltonian considered in [28,29] is of the Gustavson type (1), thus rendering ${\cal A}_m$ diagonal. As explained in the appendix, for magnetic bottle Hamiltonians ${\cal A}_m$ is not diagonal, which makes the determination of the splitting (12) and the inversion of (14) a much more difficult task.