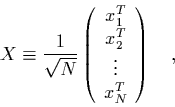


Next: Singular Value Decomposition as
Up: Singular System Analysis
Previous: Singular System Analysis
Contents
As a first step we choose some  . We want to embed
. We want to embed 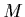 in
in
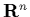 . In general
. In general 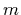 will be unknown so that it is not obvious how
to meet Takens' condition
will be unknown so that it is not obvious how
to meet Takens' condition 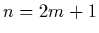 . But if we choose
. But if we choose  large enough to
ensure that
large enough to
ensure that 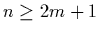 then we can embed
then we can embed 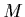 in
in 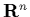 ,
according to Takens' theorem 2, because it is a well known fact that
every Euclidean space
,
according to Takens' theorem 2, because it is a well known fact that
every Euclidean space
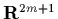 can again be embedded in any
higher-dimensional Euclidean space
can again be embedded in any
higher-dimensional Euclidean space 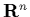 without any problems.
So we start by making an ansatz for
without any problems.
So we start by making an ansatz for  and our concern for the
next few paragraphs will be to find a more appropriate
and our concern for the
next few paragraphs will be to find a more appropriate 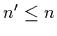 such that
such that 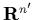 is a space containing Takens' embedding space.
Thus
is a space containing Takens' embedding space.
Thus 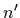 will be a better embedding dimension than the
will be a better embedding dimension than the  we started
with, since it gives a lower-dimensional embedding space.
We want to use the method of delays to construct vectors in
we started
with, since it gives a lower-dimensional embedding space.
We want to use the method of delays to construct vectors in 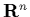 from the
from the 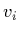 of the time series. Doing this one realizes that there is
even one more quantity which is not yet specified: One could, for example,
take the series of
of the time series. Doing this one realizes that there is
even one more quantity which is not yet specified: One could, for example,
take the series of  -vectors
-vectors
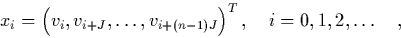 |
(27) |
which we are obviously allowed to use in accordance with Takens'
statements. So we also have to choose the ``lag time''
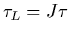 , where
, where 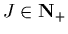 . We will see in section 3.4.2
that we do not have to spend much effort on choosing
. We will see in section 3.4.2
that we do not have to spend much effort on choosing 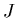 :
when we use the singular systems technique the
influence of the lag time becomes insignificant, hence we will choose it
from now on to equal
:
when we use the singular systems technique the
influence of the lag time becomes insignificant, hence we will choose it
from now on to equal  (i.e.
(i.e. 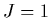 ).
Consider a sequence of
).
Consider a sequence of 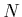 vectors
vectors
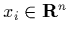 ,
,
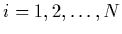 (i.e. we take a time series containing
(i.e. we take a time series containing 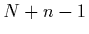 data
points)12.
There seems to be no analytical way to compute the proper (i.e.
minimal) embedding
dimension from the time series. However, it is possible to determine a
reasonable estimate for it: For some given
data
points)12.
There seems to be no analytical way to compute the proper (i.e.
minimal) embedding
dimension from the time series. However, it is possible to determine a
reasonable estimate for it: For some given  the
the  -vectors
-vectors 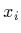 usually do not explore the whole space
usually do not explore the whole space 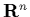 . Rather than that they
are restricted to some subspace
. Rather than that they
are restricted to some subspace 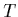 of
of 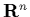 ; T contains the
embedded manifold
; T contains the
embedded manifold 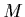 which contains the picture of the attractor:
which contains the picture of the attractor:
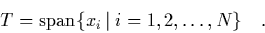 |
(28) |
When we assume that
the 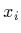 really visit the whole attractor in the
embedding space (more or less) uniformly and we bear in mind that
really visit the whole attractor in the
embedding space (more or less) uniformly and we bear in mind that
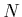 usually is much larger than
usually is much larger than  then
then
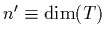 is a sensible
upper bound for the minimal embedding dimension. In order to determine
is a sensible
upper bound for the minimal embedding dimension. In order to determine 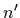 we
compute the maximum number of linearly independent vectors that can be
constructed as linear combinations of the
we
compute the maximum number of linearly independent vectors that can be
constructed as linear combinations of the 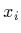 . To do this, we define the
. To do this, we define the
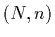 -trajectory matrix
-trajectory matrix 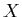 :
:
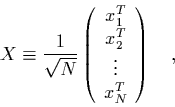 |
(29) |
which is built out of all vectors we want to use to reconstruct the
attractor.
Notice that when operating with 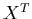 on some
on some 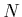 -vector we get an
-vector we get an
 -vector:
-vector:
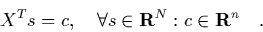 |
(30) |
Since we are interested in linearly independent  -vectors, we choose a
set of vectors
-vectors, we choose a
set of vectors
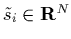 such that the
such that the  -vectors
-vectors
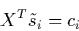 |
(31) |
are orthonormal. We introduce some real constants
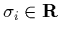 into this equation, in order to normalize the
into this equation, in order to normalize the 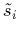 :
:
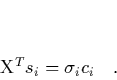 |
(32) |
The important point about this equation is that, after transposing, it
can be rewritten as
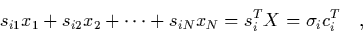 |
(33) |
i.e. as a linear combination of the reconstructed trajectory vectors.
This tells us, when we keep in mind the definition of 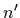 , that we can
get
, that we can
get 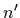 linearly independent vectors
linearly independent vectors 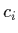 , using eq. (34); so we
have
, using eq. (34); so we
have 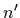 vectors
vectors 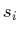 and
and 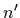 numbers
numbers
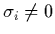 , too. The
, too. The
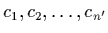 are elements of an orthonormal basis
are elements of an orthonormal basis
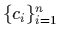 of
of 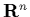 .
Thus we are left to determine
.
Thus we are left to determine 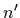 as the number of those
as the number of those 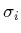 which
are non-zero.
Define the structure matrix
which
are non-zero.
Define the structure matrix
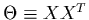 ; then it follows
from eq. (34) that the
; then it follows
from eq. (34) that the 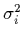 are the eigenvalues of this
matrix:
are the eigenvalues of this
matrix:
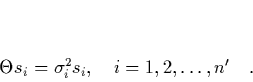 |
(34) |
We could determine 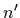 as the number of the non-zero eigenvalues of
as the number of the non-zero eigenvalues of
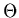 . But
. But 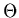 is a huge
is a huge 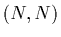 -matrix, and singular, and its
diagonalization is in practice impossible. Instead, we notice that the
covariance matrix
-matrix, and singular, and its
diagonalization is in practice impossible. Instead, we notice that the
covariance matrix
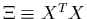 has the same non-zero
eigenvalues as
has the same non-zero
eigenvalues as 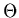 , and
, and 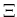 is much easier to diagonalize, because it is only an
is much easier to diagonalize, because it is only an 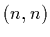 -matrix. So
all one has to do in order to calculate
-matrix. So
all one has to do in order to calculate 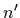 which, cum grano salis,
estimates the minimal embedding dimension
which, cum grano salis,
estimates the minimal embedding dimension 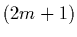 , is to determine the
number of the non-zero eigenvalues of
, is to determine the
number of the non-zero eigenvalues of
 |
(35) |
Now we know that the trajectory is confined to an 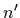 -dimensional
subspace of
-dimensional
subspace of 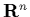 , and we can use
, and we can use 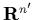 as the embedding
space.
However, this treatment only makes sense in the case that we have noise-
free data.
as the embedding
space.
However, this treatment only makes sense in the case that we have noise-
free data.
Footnotes
- ...
points)12
-
We will generally assume
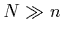 , which is obviously true in most
cases.
, which is obviously true in most
cases.



Next: Singular Value Decomposition as
Up: Singular System Analysis
Previous: Singular System Analysis
Contents
Martin_Engel
2000-05-25