


Next: Choice of First Embedding
Up: Singular System Analysis
Previous: Choice of a Proper
Contents
We will see that in the presence of noise one has to expect that all zero
eigenvalues 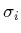 (of the noise-free case) will be changed into
non-zero numbers, small but non-zero! So the simple method of the above
section breaks down and the result of the computation will be in almost
all cases
(of the noise-free case) will be changed into
non-zero numbers, small but non-zero! So the simple method of the above
section breaks down and the result of the computation will be in almost
all cases 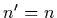 , no matter how large
, no matter how large  is.
To deal with this problem we introduce two new matrices
is.
To deal with this problem we introduce two new matrices
The elements 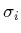 of
of 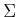 are called the singular values
of
are called the singular values
of 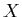 . Using these definitions, the definition of
. Using these definitions, the definition of 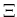 and eq.
(34) we get the important relation
and eq.
(34) we get the important relation
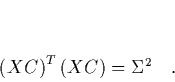 |
(38) |
Recall that
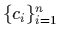 is by definition an orthonormal basis of
is by definition an orthonormal basis of
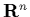 . So the
. So the 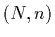 -matrix
-matrix
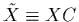 can be interpreted
as the projection of the trajectory matrix onto this new basis. Then
can be interpreted
as the projection of the trajectory matrix onto this new basis. Then
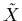 is the trajectory matrix expressed in the basis
is the trajectory matrix expressed in the basis 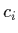 , and
, and
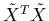 in the above equation is the covariance matrix in
the same new basis. If one considers the general form of a covariance
matrix,
in the above equation is the covariance matrix in
the same new basis. If one considers the general form of a covariance
matrix,
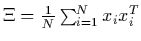 , then it is clear that
, then it is clear that
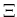 measures the correlation of all the vectors
measures the correlation of all the vectors 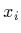 , averaged over
the entire trajectory. Thus the fact that the product
, averaged over
the entire trajectory. Thus the fact that the product
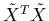 gives a
diagonal matrix (eq. (40)) shows that in the basis
gives a
diagonal matrix (eq. (40)) shows that in the basis 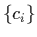 the vectors of the trajectory (
the vectors of the trajectory (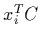 ) are uncorrelated 13.
What is more, we can see from eq. (40) that
) are uncorrelated 13.
What is more, we can see from eq. (40) that 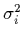 is
proportional to the extent to which the trajectory varies in the
is
proportional to the extent to which the trajectory varies in the
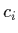 -direction. One can think of the trajectory as exploring on the
average an ellipsoid in
-direction. One can think of the trajectory as exploring on the
average an ellipsoid in 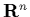 , the directions and lengths of the
axes of which are given by the
, the directions and lengths of the
axes of which are given by the 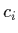 and the
and the 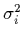 , respectively.
This picture is very valuable for the discussion of the effect of noise
on the trajectory: If there is, for example, a floor of white noise
(i.e. we have
, respectively.
This picture is very valuable for the discussion of the effect of noise
on the trajectory: If there is, for example, a floor of white noise
(i.e. we have
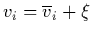 , where
, where
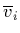 is the
deterministic contribution to the observable and
is the
deterministic contribution to the observable and 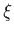 stands for the
noise) then we get for the covariance matrix an expression like
stands for the
noise) then we get for the covariance matrix an expression like
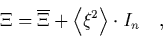 |
(39) |
where
 denotes the time average,
denotes the time average, 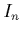 is the
is the
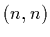 -identity matrix and
-identity matrix and 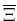 is the deterministic
contribution we have discussed until now. Diagonalization of
is the deterministic
contribution we have discussed until now. Diagonalization of 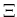 for
this ``white noise case'' yields the eigenvalues
for
this ``white noise case'' yields the eigenvalues
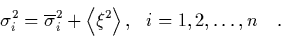 |
(40) |
Notice that in the presence of noise all eigenvalues are non-zero
(since
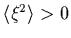 ), even
for those directions
), even
for those directions 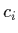 which are not explored by the deterministic
movement of the system. Thus the influence of noise on our analysis is to
make us think that the (deterministic) trajectory explores all
directions of
which are not explored by the deterministic
movement of the system. Thus the influence of noise on our analysis is to
make us think that the (deterministic) trajectory explores all
directions of 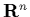 , instead of only
, instead of only 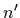 !
The solution of this problem is found by considering the singular
value decomposition of
!
The solution of this problem is found by considering the singular
value decomposition of 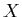 :
:
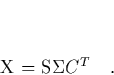 |
(41) |
(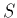 is the
is the 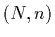 -matrix formed of the eigenvectors of
-matrix formed of the eigenvectors of 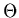 .) We
will see below that this decomposition is useful, because
.) We
will see below that this decomposition is useful, because 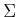 appears as one of
the factors constituting
appears as one of
the factors constituting 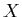 . We want to find those entries of
. We want to find those entries of
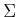 which are obviously non-zero only due to the effects of
noise. One possibility to do this is to measure, in addition to the true
time series, a time series which consists only of the noise and then to
compute the corresponding mean square projections onto the
which are obviously non-zero only due to the effects of
noise. One possibility to do this is to measure, in addition to the true
time series, a time series which consists only of the noise and then to
compute the corresponding mean square projections onto the
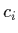 -directions
(which we found for the true time series). These quantities are to
be compared with the respective
-directions
(which we found for the true time series). These quantities are to
be compared with the respective 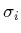 (of the true time series) and
if both are found to be of
the same order of magnitude then we know that this particular
(of the true time series) and
if both are found to be of
the same order of magnitude then we know that this particular 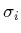 is only non-zero due to the noise; in other words, the corresponding
direction
is only non-zero due to the noise; in other words, the corresponding
direction 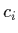 is noise-dominated. A straightforward strategy (which
uses the special form of eq. (43)) to get
rid of this most significant
influence of noise is to set those selected entries equal to
zero14. Thus we arrive at the following corrected equation for the approximate
deterministic part
is noise-dominated. A straightforward strategy (which
uses the special form of eq. (43)) to get
rid of this most significant
influence of noise is to set those selected entries equal to
zero14. Thus we arrive at the following corrected equation for the approximate
deterministic part 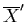 of the trajectory matrix:
of the trajectory matrix:
(Notice that the
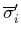 are not the deterministic
component
are not the deterministic
component
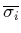 of the
of the 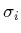 ; but, by construction,
; but, by construction,
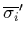 and
and
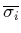 should be approximately the same.),
which can be simplified to get a representation of the corrected trajectory
matrix
should be approximately the same.),
which can be simplified to get a representation of the corrected trajectory
matrix 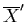 which is most easy to work with:
which is most easy to work with:
 |
(45) |
This equation is nice to work with since the 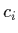 and
and 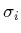 are easy
to compute by diagonalization of the covariance matrix.
The sum in eq. (47) will run over
are easy
to compute by diagonalization of the covariance matrix.
The sum in eq. (47) will run over 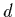 summands, and of course we
expect
summands, and of course we
expect 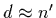 . We relabel the
. We relabel the
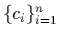 such that the
first
such that the
first 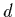 of them correspond to those eigenvalues
of them correspond to those eigenvalues 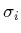 which are not
noise-dominated. Then we know, after having eliminated the effect
of noise as far as possible, that the trajectory is confined to a
which are not
noise-dominated. Then we know, after having eliminated the effect
of noise as far as possible, that the trajectory is confined to a
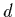 -dimensional subspace of
-dimensional subspace of 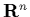 which is spanned by
which is spanned by
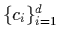 . So we can take
. So we can take 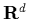 as the embedding space
instead of
as the embedding space
instead of 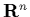 .
Finally we get the following vectors on the trajectory in
.
Finally we get the following vectors on the trajectory in 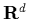 :
:
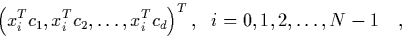 |
(46) |
and it is these vectors which we can now plot in 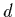 dimensions (taking
e.g. two- or three-dimensional cross-sections) to get the geometric
picture of the attractor which we have been aiming at.
dimensions (taking
e.g. two- or three-dimensional cross-sections) to get the geometric
picture of the attractor which we have been aiming at.
Footnotes
- ... uncorrelated13
-
This result justifies the choice
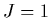 in section 3.1: since in a
well-chosen basis (
in section 3.1: since in a
well-chosen basis (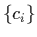 ) the vectors which form the trajectory are
uncorrelated, the lag-time does not influence our results and we can
choose it at our convenience.
) the vectors which form the trajectory are
uncorrelated, the lag-time does not influence our results and we can
choose it at our convenience.
- ...
zero14
-
One should be aware of the fact that this strategy does not remove
all effects of the noise on the trajectory: The noise contribution
to those
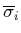 which are non-zero according to
eq. (46) remains unchanged. It is not totally
clear to me why Broomhead and King in [7] do not propose to
subtract the noise
floor from all eigenvalues
which are non-zero according to
eq. (46) remains unchanged. It is not totally
clear to me why Broomhead and King in [7] do not propose to
subtract the noise
floor from all eigenvalues 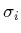 by replacing
by replacing 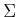 in
eq. (43) with
in
eq. (43) with
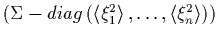 (or with
(or with
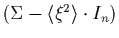 in the case of white
noise);
this would (on the average!) remove the noise floor from all eigenvalues.
Maybe the reason for not doing this are:
in the case of white
noise);
this would (on the average!) remove the noise floor from all eigenvalues.
Maybe the reason for not doing this are:
 we would not get eq. (47) in this nice form which
is easy to handle numerically;
we would not get eq. (47) in this nice form which
is easy to handle numerically;
 the effect of noise on the first
the effect of noise on the first 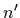 components is assumed to
be not very large;
components is assumed to
be not very large;
 for the calculation of
for the calculation of 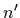 the numerical values of the
the numerical values of the
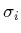 do not matter anyhow, apart from being above or in the
noise floor.
do not matter anyhow, apart from being above or in the
noise floor.



Next: Choice of First Embedding
Up: Singular System Analysis
Previous: Choice of a Proper
Contents
Martin_Engel
2000-05-25