


Next: Conclusion
Up: Analysis of Real-World Data
Previous: Choice of First Embedding
Contents
The question of how many reconstructed phase space vectors (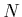 ) we need
to secure
that the reconstructed picture of the attractor is ``accurate'' is seldom
addressed in the literature. Often it is simply implicitely assumed that
) we need
to secure
that the reconstructed picture of the attractor is ``accurate'' is seldom
addressed in the literature. Often it is simply implicitely assumed that
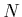 is large enough to make the error small. It is clear (when keeping
Takens' results in mind) that for
is large enough to make the error small. It is clear (when keeping
Takens' results in mind) that for 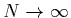 our picture converges to
an object which is (diffeomorphically) equivalent to the attractor. We
will take a brief look on what is known about the requirements on
our picture converges to
an object which is (diffeomorphically) equivalent to the attractor. We
will take a brief look on what is known about the requirements on 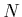 to
come as near to this ideal as possible.
The first thing to mention is that the needed
to
come as near to this ideal as possible.
The first thing to mention is that the needed 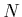 depends on the
``fractality'' of the attractor, that is the more complex the attractor is
(i.e. the larger the modulus of the difference between the attractor's
dimension and the nearest integer is)
the more points we need to reproduce it correctly. Secondly the
attractor-picture is not only constructed as an end in itself but to
derive characteristic properties from it. From this it follows that one
should choose
depends on the
``fractality'' of the attractor, that is the more complex the attractor is
(i.e. the larger the modulus of the difference between the attractor's
dimension and the nearest integer is)
the more points we need to reproduce it correctly. Secondly the
attractor-picture is not only constructed as an end in itself but to
derive characteristic properties from it. From this it follows that one
should choose 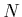 according to the quantity to be computed. For example,
calculations of Lyapunov exponents usually require more data points than
calculations of the correlation dimension. Thirdly, an inhomogeneous
distribution of the
according to the quantity to be computed. For example,
calculations of Lyapunov exponents usually require more data points than
calculations of the correlation dimension. Thirdly, an inhomogeneous
distribution of the 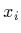 on the reconstructed attractor obviously results
in the need for more data points, since we want to resolve all parts of
the attractor accurately enough.
Considering the above hints which seem to suggest that
usually a large
on the reconstructed attractor obviously results
in the need for more data points, since we want to resolve all parts of
the attractor accurately enough.
Considering the above hints which seem to suggest that
usually a large 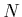 is required it is good news that one can conclude from
systematic studies surveyed by Albano et al. [8] that often a
surprisingly small number of data points is sufficient, especially when one
computes numerically robust quantities such as the correlation dimension.
Unfortunately this observation seems to be correct only if the required
accuracy is small. If one wants to compute for instance dimensions up to
several decimal places then it can become necessary to use millions of
data points. This observation is illustrated by the numerical experiment
with the Rössler system, mentioned above: Although the geometrical
structures of the objects in Figs. 5.a/5.b and e.g. in Fig. 5.f/5.g are
very similar, one cannot expect to derive very accurate numerical
invariants from the latter ones, since they are quite coarse-grained.
Much more effort must be spent on slightly more exact computations.
is required it is good news that one can conclude from
systematic studies surveyed by Albano et al. [8] that often a
surprisingly small number of data points is sufficient, especially when one
computes numerically robust quantities such as the correlation dimension.
Unfortunately this observation seems to be correct only if the required
accuracy is small. If one wants to compute for instance dimensions up to
several decimal places then it can become necessary to use millions of
data points. This observation is illustrated by the numerical experiment
with the Rössler system, mentioned above: Although the geometrical
structures of the objects in Figs. 5.a/5.b and e.g. in Fig. 5.f/5.g are
very similar, one cannot expect to derive very accurate numerical
invariants from the latter ones, since they are quite coarse-grained.
Much more effort must be spent on slightly more exact computations.



Next: Conclusion
Up: Analysis of Real-World Data
Previous: Choice of First Embedding
Contents
Martin_Engel
2000-05-25