


Next: Basic Remarks about the
Up: Time Series Analysis A
Previous: Theoretical Foundation - Takens'
Contents
So far, the method of delays remains ill-defined since it does not take
into account the practical obstacles which arise: generally, the dimension
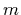 of
of 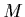 is not known a priori, so the choice of a proper embedding
dimension
is not known a priori, so the choice of a proper embedding
dimension  is a problem.
is a problem.
Also, instead of having the infinitely long time series considered by
Takens one works in practice with a time series of finite length (from
which we construct a series of 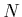 vectors with the method of delays),
so we need to find a criterion for the smallest number of data points
required to get ``good'' results.
vectors with the method of delays),
so we need to find a criterion for the smallest number of data points
required to get ``good'' results.
Takens' theory does not say anything about the sampling time  between two successive measurements. (It has not been necessary so far to
say something
about it, because for
between two successive measurements. (It has not been necessary so far to
say something
about it, because for 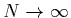 generically any value of
generically any value of  can be
taken.) For a real data set
can be
taken.) For a real data set 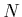 is finite, so we cannot expect any more
that every sampling time will give good results. We must assign a
suitable value to
is finite, so we cannot expect any more
that every sampling time will give good results. We must assign a
suitable value to  .
.
Additionally, all data, no matter if it is taken from numerical or
physical experiments, will be noisy (i.e. it will be measured with finite
precision only) and we must consider this problem when building our
strategy of data analysis.
Subsections



Next: Basic Remarks about the
Up: Time Series Analysis A
Previous: Theoretical Foundation - Takens'
Contents
Martin_Engel
2000-05-25