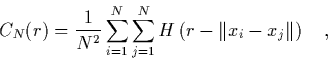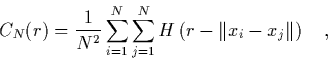


Next: Singular System Analysis
Up: Analysis of Real-World Data
Previous: Topological Considerations
Contents
One of the many quantities which are usually used to characterize a
strange attractor is the correlation dimension. It was introduced by
Grassberger and Procaccia as a measure of strangeness which is easier to
handle (especially numerically) than the measures used until then
[5,6].
For instance, if the dynamical laws of a system are not known then
the Hausdorff dimension is usually computed using box-counting algorithms
(see for example [14], chapter 3.3).
These are very time-consuming, especially for higher-dimensional
systems, because the number of calculations grows exponentially with the
dimension [5,6,8]. The problems we encounter for
our special case of analyzing a dynamical system where the only
information about the system is given in the form of a time series are
even larger, since we have to go through the embedding process first.
Grassberger and Procaccia suggested to use, instead of the Hausdorff
dimension, the correlation dimension 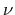 , which can be computed
directly from the time series without greater difficulties. We will see
that calculation of
, which can be computed
directly from the time series without greater difficulties. We will see
that calculation of 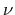 will provide us with a method to find a proper
embedding dimension ([8] and [14], chapter 5.3), as
well.
To determine the correlation dimension we first calculate the
correlation integral:
will provide us with a method to find a proper
embedding dimension ([8] and [14], chapter 5.3), as
well.
To determine the correlation dimension we first calculate the
correlation integral:
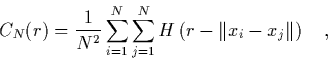 |
(25) |
where 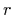 is the correlation length and
is the correlation length and 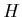 the Heaviside function. For
the Heaviside function. For
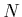 sufficiently large and
sufficiently large and 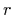 sufficiently small the logarithm of
sufficiently small the logarithm of
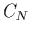 as a function of the logarithm of
as a function of the logarithm of 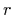 will have a linear region, the
scaling region, and the slope in this region is the correlation
dimension
will have a linear region, the
scaling region, and the slope in this region is the correlation
dimension 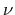 :
:
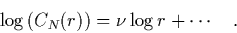 |
(26) |
Because  is closely related to the Hausdorff-dimension11 which itself is a generalization of the intuitive concept of
dimensionality [17],
it seems sensible to apply a procedure similar to the one
presented in the previous section [8]: We calculate
is closely related to the Hausdorff-dimension11 which itself is a generalization of the intuitive concept of
dimensionality [17],
it seems sensible to apply a procedure similar to the one
presented in the previous section [8]: We calculate  for
a sequence of embedding dimensions
for
a sequence of embedding dimensions  and infer the respective
and infer the respective
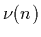 's. We expect that if the embedding dimension is too small then
's. We expect that if the embedding dimension is too small then
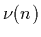 equals
equals  . (In this case
. (In this case 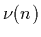 is not the true correlation dimension of the attractor but only an
artefact, due to the embedding dimension being too small.) So increasing
is not the true correlation dimension of the attractor but only an
artefact, due to the embedding dimension being too small.) So increasing
 yields an increasing
yields an increasing 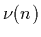 . But for
. But for  sufficiently large
sufficiently large
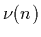 will be smaller than
will be smaller than  and equal to the true correlation
dimension. A further increase should not change the value of
and equal to the true correlation
dimension. A further increase should not change the value of 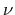 any
more.
Thus we have a method to compute the proper embedding dimension: we simply
use the correlation dimension as the embeding dimension.
any
more.
Thus we have a method to compute the proper embedding dimension: we simply
use the correlation dimension as the embeding dimension.
Footnotes
- ... Hausdorff-dimension11
-
For the relationship of
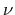 to the Hausdorff and information
dimensions see [5,6]; Schuster [14], chapter
5.3, shows that these
three types of dimensions can be organized within the framework of
generalized dimensions
to the Hausdorff and information
dimensions see [5,6]; Schuster [14], chapter
5.3, shows that these
three types of dimensions can be organized within the framework of
generalized dimensions 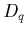 :
: 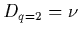 , for example. It seems
to be true that in most cases
all three dimensions do not differ very much and often they are even the
same, e.g. when the attractor is covered uniformly by the
, for example. It seems
to be true that in most cases
all three dimensions do not differ very much and often they are even the
same, e.g. when the attractor is covered uniformly by the  [6].
[6].



Next: Singular System Analysis
Up: Analysis of Real-World Data
Previous: Topological Considerations
Contents
Martin_Engel
2000-05-25