The Stochastic Web

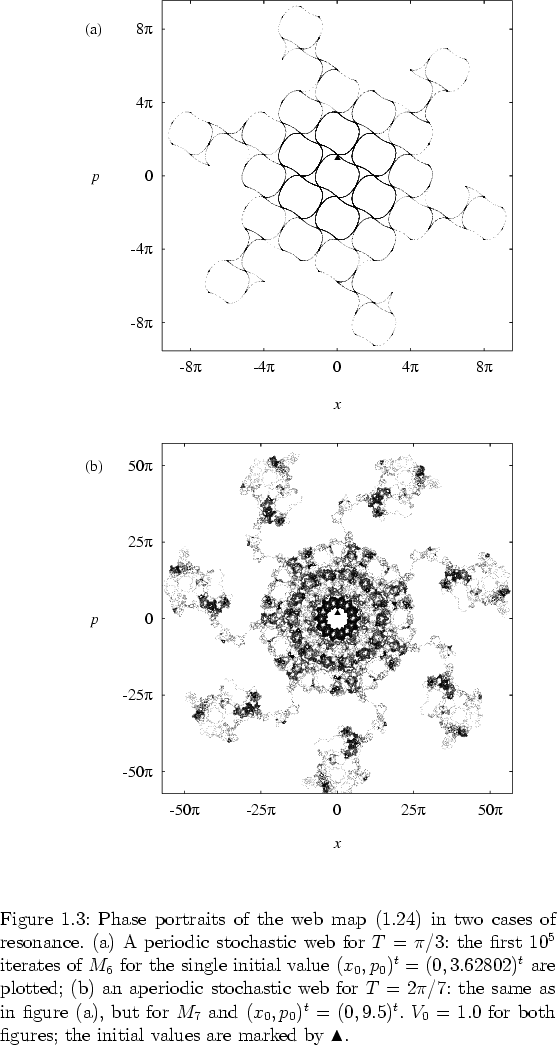
Two examples of stochastic webs that are generated by the web map (1.24) are shown in figure 1.3.

The figures each show the first $10^5$ iterates of the web map $M_q$ for a single initial value. In figure 1.3a, for $q=6$ ($T=\pi /3$), the iterates form a regular web-like pattern, which in this case is called a kagome lattice [ZSUC91]. The complete kagome lattice, which covers the entire phase plane, is obtained by iterating the map ``infinitely often''. As I discuss in more detail in the following subsections, the dynamics of the web map on this lattice is (weakly) chaotic, thus giving rise to the name stochastic web.

Certain (approximate) symmetry properties of the stochastic web for $q=6$ are obvious: in this particular case the web is characterized by translational symmetry in two transversal directions (e.g. given by $(2\pi,\pm 2\pi/\sqrt{3})^t$) and by rotational symmetry with respect to several classes of 2-fold rotations, in addition to several reflection and glide reflection symmetries. In fact it turns out that the underlying skeleton of the web is even invariant under 2-fold, 3-fold and 6-fold rotations about suitably chosen centres of rotation. See subsection 1.2.2 for a rigorous definition of the skeletons of stochastic webs, and for more information on the symmetry groups of these skeletons.

In figure 1.3b, for $q=7$ ($T=2\pi /7$), the situation is different: although this phase portrait still reveals approximate rotational invariance with respect to the origin (rotations through the angle $2\pi/7$), there is no translational invariance as seen for example in figure 1.3a. In this sense, the phase portrait in figure 1.3b is less regular than that in figure 1.3a. Webs in phase space with just rotational symmetry -- like the web for $q=7$ -- are called aperiodic stochastic webs, as opposed to the periodic stochastic webs exhibiting both rotational and translational symmetry, an example being the web for $q=6$.

Having introduced periodic and aperiodic stochastic webs, the importance of the resonance condition (1.23) may now be illustrated by considering a value of $T=2\pi/q$ with noninteger $q$. Figure 1.4 shows a phase portrait of the POINCARÉ map (1.21) for $T=1.0$.

Although this value of $T$ is fairly close to $\pi/3\approx 1.05$, the phase portraits for these two values of $T$ are significantly different (cf. figure 1.3a). In the nonresonance case the phase space structures reveal much less regularity: the whole phase plane -- with the exception of a region near the origin where some invariant lines persist -- forms a single dynamically connected chaotic region without an obvious inner structure, apart from variations in the density of points which are probably due to cantori.

In the following subsection 1.2.1 I present an argument for the fact that periodic webs, characterized by both rotational and translational symmetries, can develop not for all $q\in\mathbb{N}$ but only for a few specific values of $q$, namely for

$$q \in {\mathcal Q}:= \{ 1,2,3,4,6 \};$$ (1.18)

in the present study I mainly concentrate the attention on these particular cases.

I then proceed in subsection 1.2.2 to the discussion of the skeleton, or ``backbone'', of the web and derive an equation that determines this overall structure of the web. Finally, in subsections 1.2.3 and 1.2.4 I briefly give an overview on what is known about the classical unbounded diffusive dynamics within the channels of the web that form around its skeleton; in particular I discuss the typical energy growth of a diffusing particle and the width of the channels of diffusive dynamics which is directly controlled by the kick strength $V_0$. The results presented in subsections 1.2.2 and 1.2.3 are mainly based on [ZSUC91].