In the theory of stochastic webs one is mainly interested
in the
symmetrical
dynamical patterns that evolve in the phase plane as a result
of the dynamics of the kicked harmonic oscillator.
The types of symmetry that can be of interest here are determined by
the symmetry groups
admitted by
the Hamiltonian (1.17).
Its first part describes a rotation with unit
angular velocity in the phase plane; as this rotation is interrupted by
the kicks stroboscopically, with time constant
![]() ,
one can
expect rotational
symmetries
through
the angle
,
one can
expect rotational
symmetries
through
the angle
![]() (and integer multiples
thereof),
i.e.
(and integer multiples
thereof),
i.e. ![]() -fold rotation invariances.
The second part of the Hamiltonian (1.17), describing the kicks,
exhibits
translational
invariance with respect to shifts
-fold rotation invariances.
The second part of the Hamiltonian (1.17), describing the kicks,
exhibits
translational
invariance with respect to shifts
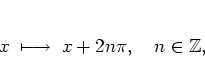 |
(1.19) |
Before taking into account the characteristic properties of the kicked harmonic oscillator (1.17), it is useful to determine what kinds of both rotationally and translationally invariant tilings of a two-dimensional plane are possible at all [Wey82]. See also [Lam93,LQ94,Jun95] for a more general exposition of this topic. The symmetry groups describing such tilings are the planar space groups or wallpaper groups [GS87].1.4
Consider a set of points ![]() in the plane that is invariant both with
respect
to translations by the arbitrary period
in the plane that is invariant both with
respect
to translations by the arbitrary period ![]() in some direction
and with respect to rotations
through
the
angle
in some direction
and with respect to rotations
through
the
angle ![]() about the points of
about the points of ![]() .
Those
.
Those ![]() that fit into this setting are to be identified now.
Depending on the value of
that fit into this setting are to be identified now.
Depending on the value of ![]() , there may be a single or two
transversal directions of translation invariance.
, there may be a single or two
transversal directions of translation invariance.
Let ![]() and
and ![]() be elements of
be elements of ![]() .
Submitting these points to rotations
through
.
Submitting these points to rotations
through
![]() about the points
about the points ![]() and
and ![]() , respectively,
the points
, respectively,
the points ![]() and
and ![]() are obtained
(see figure 1.5),
are obtained
(see figure 1.5),
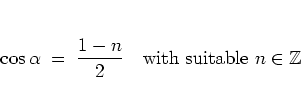 |
(1.20) |
![[*]](crossref.png) ; frequently used synonymous
terms are ``uniform stochastic webs'' or ``stochastic webs with crystal
symmetry''.
The aperiodic stochastic webs obtained for
; frequently used synonymous
terms are ``uniform stochastic webs'' or ``stochastic webs with crystal
symmetry''.
The aperiodic stochastic webs obtained for
Although the webs for
![]() and
and
![]() share their general
web-like structure, they are fundamentally different beyond the issue
of periodicity: The width of the
channels of the latter
typically
decreases with the distance from the origin of
the phase plane, whereas the periodicity of the first guarantees that
the width of the channels is the same around every mesh of the web.
Numerous examples of webs with quasicrystal symmetry can be found in the
literature; see for example [CSUZ87,SUZ88,ZSUC88,CSUZ89,ZSUC91]
and references therein.
Aperiodic webs
play an important role in the theory of
quasicrystals in solid state physics
[HG94,Zum97] and are related to many other fields,
for example to the problem of tilings of the plane which finds its
application both in arts (see figure 1.6 for an example)
share their general
web-like structure, they are fundamentally different beyond the issue
of periodicity: The width of the
channels of the latter
typically
decreases with the distance from the origin of
the phase plane, whereas the periodicity of the first guarantees that
the width of the channels is the same around every mesh of the web.
Numerous examples of webs with quasicrystal symmetry can be found in the
literature; see for example [CSUZ87,SUZ88,ZSUC88,CSUZ89,ZSUC91]
and references therein.
Aperiodic webs
play an important role in the theory of
quasicrystals in solid state physics
[HG94,Zum97] and are related to many other fields,
for example to the problem of tilings of the plane which finds its
application both in arts (see figure 1.6 for an example)