



Next: Generalized Web Maps
Up: The Kicked Harmonic Oscillator
Previous: Canonical Formulation
Contents
Discrete Dynamics -- The Web Map
The dynamics that is generated by the Hamiltonian (1.17) can
obviously be split into two parts, namely the
trivial
dynamics of a
free harmonic oscillator between two successive kicks, and the kick
dynamics itself. Because of the stroboscopic nature of the kick it makes
sense to consider the dynamic variables 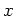 and
and 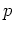 at those times only
when kicks occur. Let
at those times only
when kicks occur. Let
![\begin{subequations}
\begin{eqnarray}
x_n & := & \lim_{t\nearrow nT} x(t) \\ [0.2cm]
p_n & := & \lim_{t\nearrow nT} p(t)
\end{eqnarray}\end{subequations}](img94.png)
be the values of 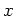 and
and 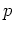 immediately before the
immediately before the 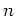 -th kick.
Then the discrete dynamics generated by (1.17)
is
given by the
POINCARÉ map1.2
-th kick.
Then the discrete dynamics generated by (1.17)
is
given by the
POINCARÉ map1.2
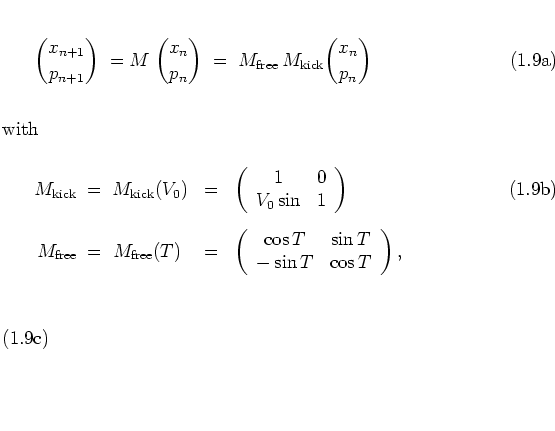
or
![\begin{displaymath}
\hspace*{-0.35cm}
\fbox{$ \displaystyle \rule[-0.85cm]{0.0...
...+ (p_n+V_0\sin x_n)\cos T.
\end{array} %
\hspace*{0.1cm}
$}
\end{displaymath}](img98.png) |
(1.9) |
Starting at the phase space point 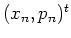 ,
first the momentum is shifted by
,
first the momentum is shifted by 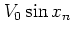 due to the kick;
then the new point
due to the kick;
then the new point
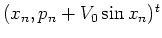 is submitted to harmonic rotation in phase space for a period of time of
length
is submitted to harmonic rotation in phase space for a period of time of
length 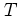 .
Figure 1.1 gives a graphical
account
of this dynamics of the map.
.
Figure 1.1 gives a graphical
account
of this dynamics of the map.
In the following I pay particular attention to the resonance
cases
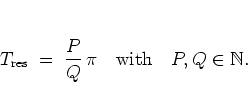 |
(1.10) |
The most important resonances are those
for which there are exactly 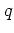 kicks per period
kicks per period 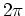 of the
unforced
oscillator:
of the
unforced
oscillator:
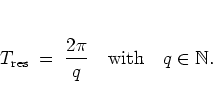 |
(1.11) |
It is
just
in these resonance cases that
a stochastic web develops, as will be seen in section
1.2.
In fact, webs with both translational and rotational symmetry can only
occur for just a few special values of 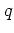 ;
this is discussed in subsection 1.2.1.
Due to this connection between stochastic webs and the map
(1.21) in
these
particular cases of resonance,
maps of this type are commonly called web maps.
(See for example [ZSUC91],
but note that there a different scaling is used.)
In the formulation used here the web map is given by
;
this is discussed in subsection 1.2.1.
Due to this connection between stochastic webs and the map
(1.21) in
these
particular cases of resonance,
maps of this type are commonly called web maps.
(See for example [ZSUC91],
but note that there a different scaling is used.)
In the formulation used here the web map is given by
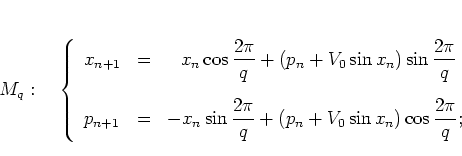 |
(1.12) |
it
depends on the two parameters
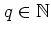 and
and
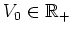 .
.
I now briefly discuss the web map for some specific values of 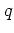 .
The case
.
The case 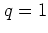 (i.e.
(i.e. 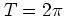 ) corresponds to cyclotron resonance,
where the frequency of the kick coincides with the frequency of the
harmonic oscillator:
) corresponds to cyclotron resonance,
where the frequency of the kick coincides with the frequency of the
harmonic oscillator:
![\begin{displaymath}
M_1: \quad
\left\{
\begin{array}{lcl}
x_{n+1} & = & x_n \\ [0.2cm]
p_{n+1} & = & p_n+V_0\sin x_n
\end{array} \right.
\end{displaymath}](img111.png) |
(1.13) |
This iteration is trivially solved by
![\begin{displaymath}
\begin{array}{lcl}
x_n & = & x_0 \; = \; \mbox{const.} \\ [0.2cm]
p_n & = & p_0+nV_0\sin x_0 \, .
\end{array}\end{displaymath}](img112.png) |
(1.14) |
In the context of the original model system of a particle moving within an
electromagnetic field
(subsection 1.1.1),
the 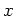 -component
of the particle
position
at times of kick is subject to uniform acceleration,
as shown in figure 1.2.
-component
of the particle
position
at times of kick is subject to uniform acceleration,
as shown in figure 1.2.
For 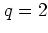 (
(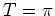 ) the dynamics is similar to that of equation (1.26): the map
is given by
) the dynamics is similar to that of equation (1.26): the map
is given by
![\begin{displaymath}
M_2: \quad
\left\{
\begin{array}{lcl}
x_{n+1} & = & -x_n...
...[0.2cm]
p_{n+1} & = & -p_n-V_0\sin x_n ,
\end{array} \right.
\end{displaymath}](img116.png) |
(1.15) |
with the explicit solution
![\begin{displaymath}
\begin{array}{lcl}
x_n & = & (-1)^n x_0 \\ [0.2cm]
p_n & = & (-1)^n \left( p_0+nV_0\sin x_0 \right).
\end{array}\end{displaymath}](img117.png) |
(1.16) |
In this case of half-integer cyclotron resonance
the particle's momentum at times of kick increases
in quite the same way as for 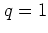 , but separately for odd and even
, but separately for odd and even 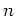 ;
the solution (1.28) can be obtained from equation
(1.26) by successively reflecting the orbit points about the
origin of phase space.
;
the solution (1.28) can be obtained from equation
(1.26) by successively reflecting the orbit points about the
origin of phase space.
Because of their evident simplicity -- in particular, the dynamics is
confined to one-dimensional lines in phase space and no two-dimensional
web structures can arise --
I do not discuss the maps 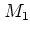 or
or 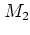 any further.
any further.
For 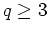 the dynamics becomes much more interesting, and complicated
structures in phase space can develop.
The most important example is the web map for
the dynamics becomes much more interesting, and complicated
structures in phase space can develop.
The most important example is the web map for 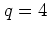 (
(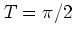 ), the dynamics of
which
has been
sketched in figure 1.1:
), the dynamics of
which
has been
sketched in figure 1.1:
![\begin{displaymath}
M_4: \quad
\left\{
\begin{array}{lcl}
x_{n+1} & = & p_n + V_0\sin x_n\\ [0.2cm]
p_{n+1} & = & -x_n.
\end{array} \right.
\end{displaymath}](img121.png) |
(1.17) |
Each kick is followed by a rotation in phase space
through
a quarter circle.
The web maps for 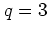 and
and 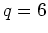 (
(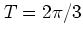 and
and 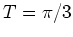 , respectively) are also of importance but not
given here explicitly, because the corresponding formulae cannot
be further simplified much beyond the form of
equation
(1.24).
, respectively) are also of importance but not
given here explicitly, because the corresponding formulae cannot
be further simplified much beyond the form of
equation
(1.24).
The structures that evolve in phase space when 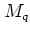 is iterated for a
large number of times
are
discussed in section
1.2,
with emphasis laid on the cases
is iterated for a
large number of times
are
discussed in section
1.2,
with emphasis laid on the cases 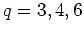 .
.
Footnotes
- ... map1.2
- Alternatively,
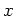 and
and 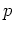 immediately
after the kicks could be considered.
The resulting POINCARÉ map
would be
topologically
conjugate to
immediately
after the kicks could be considered.
The resulting POINCARÉ map
would be
topologically
conjugate to 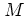 as given by
equations (1.20).
as given by
equations (1.20).




Next: Generalized Web Maps
Up: The Kicked Harmonic Oscillator
Previous: Canonical Formulation
Contents
Martin Engel 2004-01-01
![\begin{subequations}
\begin{eqnarray}
x_n & := & \lim_{t\nearrow nT} x(t) \\ [0.2cm]
p_n & := & \lim_{t\nearrow nT} p(t)
\end{eqnarray}\end{subequations}](img94.png)
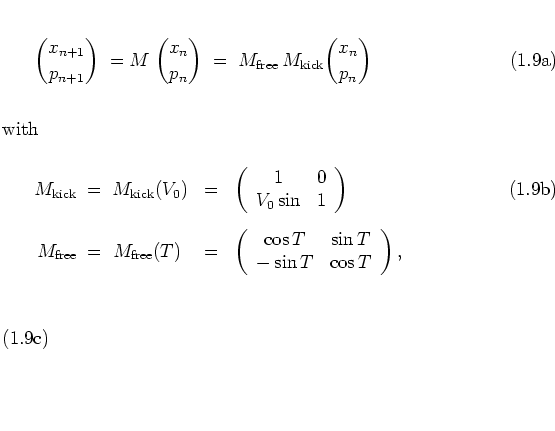
![]() and
and ![]() at those times only
when kicks occur. Let
at those times only
when kicks occur. Let
![\begin{subequations}
\begin{eqnarray}
x_n & := & \lim_{t\nearrow nT} x(t) \\ [0.2cm]
p_n & := & \lim_{t\nearrow nT} p(t)
\end{eqnarray}\end{subequations}](img94.png)
![]() and
and ![]() immediately before the
immediately before the ![]() -th kick.
Then the discrete dynamics generated by (1.17)
is
given by the
POINCARÉ map1.2
-th kick.
Then the discrete dynamics generated by (1.17)
is
given by the
POINCARÉ map1.2
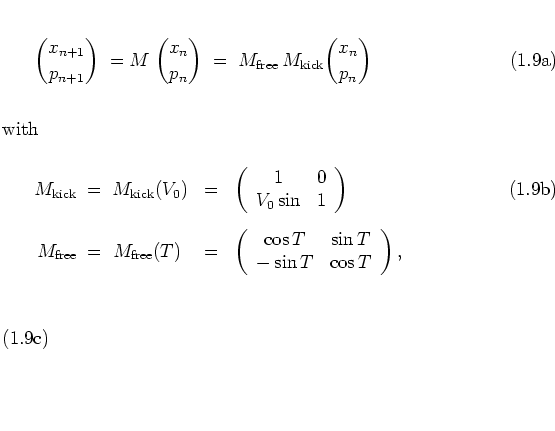
![]() .
The case
.
The case ![]() (i.e.
(i.e. ![]() ) corresponds to cyclotron resonance,
where the frequency of the kick coincides with the frequency of the
harmonic oscillator:
) corresponds to cyclotron resonance,
where the frequency of the kick coincides with the frequency of the
harmonic oscillator:
![]() (
(![]() ) the dynamics is similar to that of equation (1.26): the map
is given by
) the dynamics is similar to that of equation (1.26): the map
is given by
![]() or
or ![]() any further.
any further.
![]() the dynamics becomes much more interesting, and complicated
structures in phase space can develop.
The most important example is the web map for
the dynamics becomes much more interesting, and complicated
structures in phase space can develop.
The most important example is the web map for ![]() (
(![]() ), the dynamics of
which
has been
sketched in figure 1.1:
), the dynamics of
which
has been
sketched in figure 1.1:
![]() is iterated for a
large number of times
are
discussed in section
1.2,
with emphasis laid on the cases
is iterated for a
large number of times
are
discussed in section
1.2,
with emphasis laid on the cases ![]() .
.