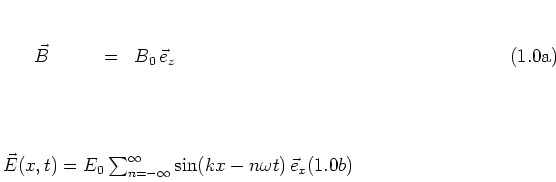
with real-valued constants
There are several different ways to motivate the discussion of the kicked harmonic oscillator. In each case it describes -- more or less approximately -- certain physical systems. In this section I discuss the most common of these model systems that finds its application for example in plasma physics [AS83]. ZASLAVSKY and co-workers discuss this approach to the problem in some detail as well [ZSUC91].
Consider the dynamics of a charged point particle in a homogeneous
stationary magnetic field ![]() and a time-dependent electric field
and a time-dependent electric field
![]() orthogonal to
orthogonal to ![]() :
:
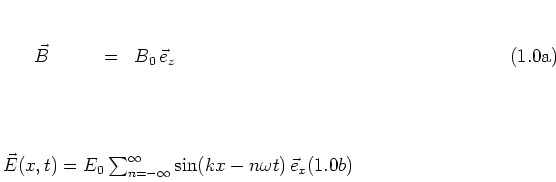
with real-valued constants
![]() .
The electric field can be interpreted as a wave packet that is periodic
both in space and time, and
that consists of
FOURIER-like components
.
The electric field can be interpreted as a wave packet that is periodic
both in space and time, and
that consists of
FOURIER-like components
![]() each
of which propagates
in
each
of which propagates
in ![]() -direction
and contributes to the complete packet with
equal
weight.
-direction
and contributes to the complete packet with
equal
weight.
Field configurations of this type can
also
be used, for instance, to describe
the beams of charged particles in storage rings under the influence of
beam-beam-interactions [Hel83,Ten83]. The applicability
in cases like this becomes more
obvious
when the
series
in equation (1.1b) is reformulated in a certain way. Taking
into account that