



Next: Canonical Formulation
Up: The Kicked Harmonic Oscillator
Previous: The Kicked Harmonic Oscillator
Contents
Newtonian Equations of Motion
Let the particle be of mass 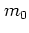 and charge
and charge 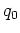 .
Then the dynamics of the
particle is governed by the Newtonian equation of motion
.
Then the dynamics of the
particle is governed by the Newtonian equation of motion
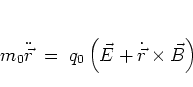 |
(1.2) |
with the vector
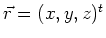 in
position space.
Using the
electromagnetic field (1.1) this yields for the components
of
in
position space.
Using the
electromagnetic field (1.1) this yields for the components
of
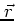 :
:
![\begin{subequations}
\begin{eqnarray}
m_0 \ddot{x} & = & q_0B_0\dot{y} + q_0E_0T...
..._0B_0\dot{x}
\\ [0.3cm]
m_0 \ddot{z} & = & 0.
\end{eqnarray}\end{subequations}](img63.png)
The dynamics in 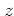 -direction is trivial (rectilinear and uniform) and
can thus be neglected.
From equation (1.5b) one obtains
-direction is trivial (rectilinear and uniform) and
can thus be neglected.
From equation (1.5b) one obtains
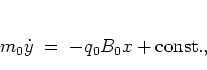 |
(1.2) |
where the constant can be set to zero without loss of generality (by an
appropriate choice of the
origin
of the 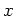 -axis). Substitution into
equation (1.5a) finally yields
-axis). Substitution into
equation (1.5a) finally yields
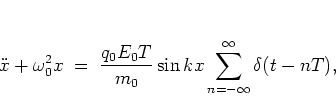 |
(1.3) |
the equation of motion of a kicked harmonic oscillator with
eigenfrequency
equal to the cyclotron frequency,
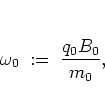 |
(1.4) |
which is
essentially given by the
magnetic field.
The right hand side of equation (1.7)
describes
the impulsive force that is driving the oscillator;
the strength of this driving is essentially determined by the amplitude of
the electric field.
The functional dependence on 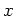 of the driving force is specified by the
kick function which in equation (1.7)
is proportional to
of the driving force is specified by the
kick function which in equation (1.7)
is proportional to 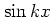 .
In subsection 1.1.4 I briefly
return to the issue of choosing the kick function
in a variety of other cases.
.
In subsection 1.1.4 I briefly
return to the issue of choosing the kick function
in a variety of other cases.
At the times 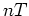 the impulse -- the kick -- changes the momentum
of the particle instantaneously, whereas its position remains unchanged.
For all other times the dynamics is just that of an unperturbed
(i.e. free) harmonic oscillator.
the impulse -- the kick -- changes the momentum
of the particle instantaneously, whereas its position remains unchanged.
For all other times the dynamics is just that of an unperturbed
(i.e. free) harmonic oscillator.




Next: Canonical Formulation
Up: The Kicked Harmonic Oscillator
Previous: The Kicked Harmonic Oscillator
Contents
Martin Engel 2004-01-01
![]() and charge
and charge ![]() .
Then the dynamics of the
particle is governed by the Newtonian equation of motion
.
Then the dynamics of the
particle is governed by the Newtonian equation of motion
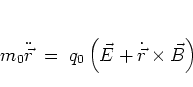
![\begin{subequations}
\begin{eqnarray}
m_0 \ddot{x} & = & q_0B_0\dot{y} + q_0E_0T...
..._0B_0\dot{x}
\\ [0.3cm]
m_0 \ddot{z} & = & 0.
\end{eqnarray}\end{subequations}](img63.png)
![]() -direction is trivial (rectilinear and uniform) and
can thus be neglected.
From equation (1.5b) one obtains
-direction is trivial (rectilinear and uniform) and
can thus be neglected.
From equation (1.5b) one obtains
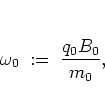
![]() the impulse -- the kick -- changes the momentum
of the particle instantaneously, whereas its position remains unchanged.
For all other times the dynamics is just that of an unperturbed
(i.e. free) harmonic oscillator.
the impulse -- the kick -- changes the momentum
of the particle instantaneously, whereas its position remains unchanged.
For all other times the dynamics is just that of an unperturbed
(i.e. free) harmonic oscillator.