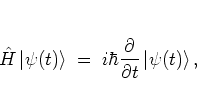 |
(2.1) |
The quantum dynamics of the unscaled kicked harmonic oscillator
with the Hamiltonian function (1.12)
is
governed
by the SCHRÖDINGER equation
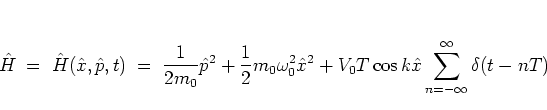 |
(2.2) |
By virtue of the scaling one is left with only the three dimensionless
parameters ![]() ,
, ![]() and
and ![]() . The first two of these describe the
nature of the kick and have to be considered both in the classical and
the quantum realms, whereas the third
-- and only the third --
is a genuinely
quantum mechanical parameter.
. The first two of these describe the
nature of the kick and have to be considered both in the classical and
the quantum realms, whereas the third
-- and only the third --
is a genuinely
quantum mechanical parameter.
As discussed in the Introduction (pages ![[*]](crossref.png) ff),
the main objective of the theory of
quantum chaos
is the investigation of the way in which the dynamics of the system
changes
when advancing from the quantum
to the classical case, i.e. when passing
from
ff),
the main objective of the theory of
quantum chaos
is the investigation of the way in which the dynamics of the system
changes
when advancing from the quantum
to the classical case, i.e. when passing
from
![]() via the semiclassical
via the semiclassical
![]() to the limiting case
to the limiting case ![]() .
.
For this purpose, comparison of the two dynamical theories of
classical and quantum mechanics, the scaling used here is more
appropriate than the one used in [BRZ91],
for example:
there, the
oscillator length
![]() is used to scale lengths, which is
a natural choice
in the quantum context, but makes
comparison with the classical case more difficult, as using this scale
in classical mechanics
does not make sense.
This problem is avoided here by measuring lengths in units of
is used to scale lengths, which is
a natural choice
in the quantum context, but makes
comparison with the classical case more difficult, as using this scale
in classical mechanics
does not make sense.
This problem is avoided here by measuring lengths in units of ![]() ,
given by the kick function, which is present in both dynamical theories
in exactly the same way.
As a result, in this scaling
the only parameter involving quantum effects is
,
given by the kick function, which is present in both dynamical theories
in exactly the same way.
As a result, in this scaling
the only parameter involving quantum effects is ![]() , and the other
two remaining parameters
, and the other
two remaining parameters ![]() and
and ![]() both play the same role classically
and quantum mechanically.
both play the same role classically
and quantum mechanically.