It is the objective of the next chapters to study the time evolution of
initial wave packets
![]() under the iteration of the quantum
map. One way to do this is to expand the initial state into a series of
eigenstates of the harmonic oscillator and then use the corresponding
matrix representation of
under the iteration of the quantum
map. One way to do this is to expand the initial state into a series of
eigenstates of the harmonic oscillator and then use the corresponding
matrix representation of ![]() for the iteration. In this subsection I
supply the formulae that are needed for this approach.
Similar results may be found in [BRZ91].
for the iteration. In this subsection I
supply the formulae that are needed for this approach.
Similar results may be found in [BRZ91].
The number states
![]() , i.e. the
eigenstates of the unkicked quantum harmonic oscillator
given by
the Hamiltonian
(2.29a),
are the solutions
of the eigenvalue equation
, i.e. the
eigenstates of the unkicked quantum harmonic oscillator
given by
the Hamiltonian
(2.29a),
are the solutions
of the eigenvalue equation
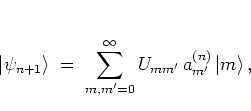 |
(2.33) |
In the harmonic oscillator eigenrepresentation the free propagator
(2.32b)
is diagonal:
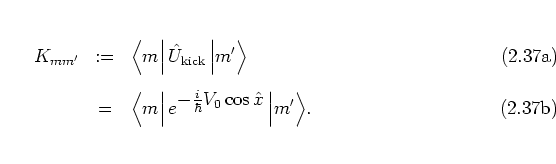
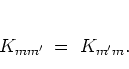 |
(2.37) |
A FOURIER expansion of
the kick propagator
![]() (cf. [AS72]) gives
(cf. [AS72]) gives
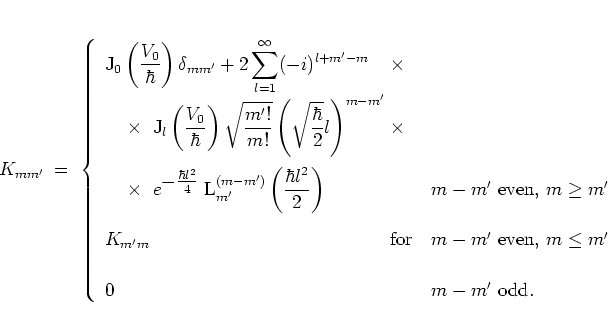
Note that
![]() for
for ![]() odd may be viewed as a
selection rule that
-- with equation (2.46b) --
follows directly from the fact that the kick potential
(1.18) has been chosen as
odd may be viewed as a
selection rule that
-- with equation (2.46b) --
follows directly from the fact that the kick potential
(1.18) has been chosen as
![]() ;
every other kick potential with the same symmetry property
-- i.e. being an even function of
;
every other kick potential with the same symmetry property
-- i.e. being an even function of ![]() --
would lead to the same selection rule.
As a result, the dynamics in the harmonic oscillator eigenrepresentation
decomposes into two parts, taking place in the dynamically disconnected
subspaces of HILBERT space that are given by the states
--
would lead to the same selection rule.
As a result, the dynamics in the harmonic oscillator eigenrepresentation
decomposes into two parts, taking place in the dynamically disconnected
subspaces of HILBERT space that are given by the states
![]() with
odd and even indices,
respectively.2.1
with
odd and even indices,
respectively.2.1
With equations (2.45) and
(2.51)
the matrix elements of the FLOQUET operator are completely specified.
For the above derivation no assumption concerning the
(resonant or nonresonant)
value of ![]() had to be made; also note that
had to be made; also note that ![]() enters
enters ![]() via the elementary exponential
via the elementary exponential
![]() in equation (2.45) only and does not interfere with the
more
complicated calculation of
in equation (2.45) only and does not interfere with the
more
complicated calculation of ![]() .
.
The rest can be left to a computer with large memory. The way in which formula (2.51) can be evaluated efficiently within a computer program is discussed in chapter 3.