It is instructive to use the quantum mechanical system introduced in the
previous section to rederive the classical POINCARÉ map
(1.21).
This is most conveniently done in the HEISENBERG picture, rather than
in the SCHRÖDINGER picture
that has been used in section 2.1 to formulate the
quantum map.
In
the present
section, and only here, I
use the indices
![]() and
and
![]() in order to distinguish between HEISENBERG and
SCHRÖDINGER operators.
(All operators
used elsewhere
without explicit reference to a particular picture
are SCHRÖDINGER operators.)
in order to distinguish between HEISENBERG and
SCHRÖDINGER operators.
(All operators
used elsewhere
without explicit reference to a particular picture
are SCHRÖDINGER operators.)
Using the time evolution operator
![]() ,
the time-dependent annihilation operator
,
the time-dependent annihilation operator
![]() can be defined as
can be defined as
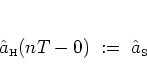 |
(2.43) |
The dynamics of
![]() is governed by the HEISENBERG equation of
motion [Mes91],
is governed by the HEISENBERG equation of
motion [Mes91],
![\begin{displaymath}
i\hbar \, \frac{{\mbox{d}}{\hat{a}_{\mbox{\tiny H}}}}{{\mbo...
...t[{\hat{a}_{\mbox{\tiny H}}},{\hat{H}_{\mbox{\tiny H}}}\right]
\end{displaymath}](img482.png) |
(2.44) |
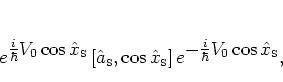
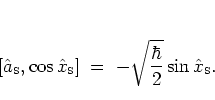 |
(2.46) |
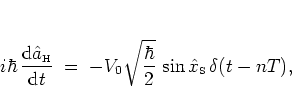 |
(2.47) |
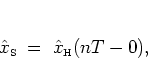 |
(2.48) |
Solving the HEISENBERG equation between two consecutive kicks,
i.e. for the unkicked harmonic oscillator, is
somewhat easier.
One has
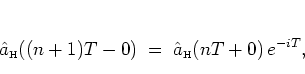 |
(2.51) |
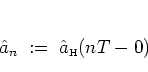 |
(2.53) |
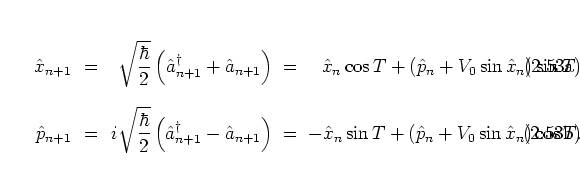
An equivalent way of deriving this form of the quantum map
is to consider
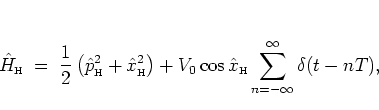 |
(2.53) |
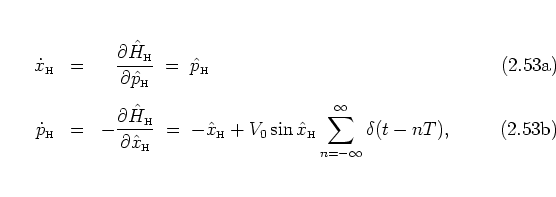
Equations (2.62) and (2.64) contain exactly the same information as their SCHRÖDINGER picture counterpart (2.37), but especially equations (2.64) are better suited than the SCHRÖDINGER picture quantum map to make contact with the classical POINCARÉ map, as I show immediately.
Substituting
formally
in the
quantum map (2.64)
the expectation values
![]() ,
,
![]() at time
at time ![]() for
the operators
for
the operators ![]() ,
, ![]() results in just the equations
(1.21) of the classical POINCARÉ map (where the expectation
values take the places of the corresponding classical observables):
results in just the equations
(1.21) of the classical POINCARÉ map (where the expectation
values take the places of the corresponding classical observables):
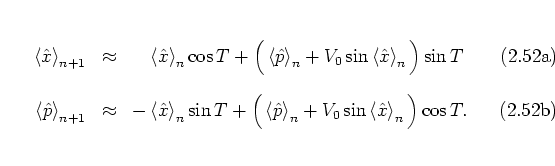
This clear formal analogy between the classical and quantum
maps
is one of the advantages of the HEISENBERG picture.
Note that the transition from the quantum mechanically exact equations
(2.64) to (2.67) is an
approximation that cannot be justified in general terms.
In fact it is
generally a quite bad approximation
the quality of which decreases with growing
![]() and
and
![]() .
.
The same
approximation
may be accomplished by replacing the operators ![]() ,
,
![]() in equation (2.62) by their
associated
in equation (2.62) by their
associated
![]() -numbers
-numbers
![]() ,
, ![]() and taking into account the relationship of these
with the classical observables
and taking into account the relationship of these
with the classical observables ![]() ,
, ![]() (or equivalently with the
action-angle variables
(or equivalently with the
action-angle variables ![]() ,
, ![]() of equation (1.35)):
of equation (1.35)):
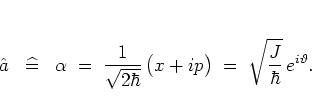 |
(2.52) |
The EHRENFEST equations of motion
of the kicked harmonic oscillator,
on the other hand, are obtained by
taking the expectation values on both sides of equations
(2.64) which gives the following, slightly different
result:
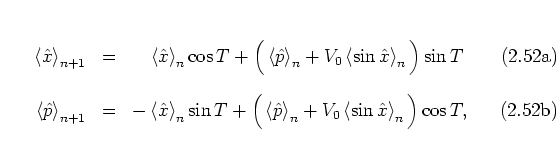
the difference being marked by the fact that in general
![]() .
Equations (2.69) are quantum mechanically exact,
in contrast to the approximative expressions
(2.67).
In the classical limit both
the position and momentum distribution become
.
Equations (2.69) are quantum mechanically exact,
in contrast to the approximative expressions
(2.67).
In the classical limit both
the position and momentum distribution become ![]() -peaked, as
they describe a single classical point particle.
In
that limit
-peaked, as
they describe a single classical point particle.
In
that limit
![]() and
and
![]() become equal and the
EHRENFEST equations coincide with
(2.67), thus becoming formally equivalent to
their classical counterparts (1.21).
become equal and the
EHRENFEST equations coincide with
(2.67), thus becoming formally equivalent to
their classical counterparts (1.21).
However, the way in which the limit of classical behaviour is reached is not obvious at all, among other reasons due to the fact that the expectation values are taken with respect to quantum states (solutions of the quantum map) about which not much is known a priori. In the following subsection I address this question from another point of view, by considering the explicit parameter dependence of the FLOQUET operator.