In the TROTTER-based algorithm, the position and momentum variables
remain
nondiscretized; only through the FFT
--
which essentially is just a sophisticated
formulation
of the discrete FOURIER transformation
using
a discrete set of nodes in position and momentum space
--
effectively ![]() and
and ![]() become discretized, too.
become discretized, too.
Now I describe a more typical finite differences approach to solving
the SCHRÖDINGER equation
for the free harmonic oscillator
in the position representation,
where both space and time are discretized in equidistant steps from the
beginning.
The solution
![]() on the interval
on the interval
![]() is
constructed at the
nodes
is
constructed at the
nodes
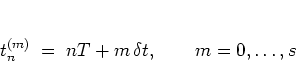 |
(3.11) |
| (3.12) | |||
| (3.13) |
In a first step,
![]() is applied to the discretized
wave function:
is applied to the discretized
wave function:
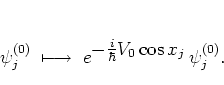 |
(3.14) |
With the discrete first order approximation for the second derivative
[SB00]
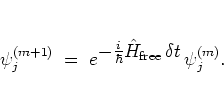 |
(3.17) |
As in the previous subsection it remains to replace the exponential
with a suitable approximant, and again using the TAYLOR formula
(3.2) is not a good choice, as it does not yield the desired
unitary
expression.
Rather, the GOLDBERG algorithm calls for the
CAYLEY form [PTVF94]
of the approximant:
With the abbreviations
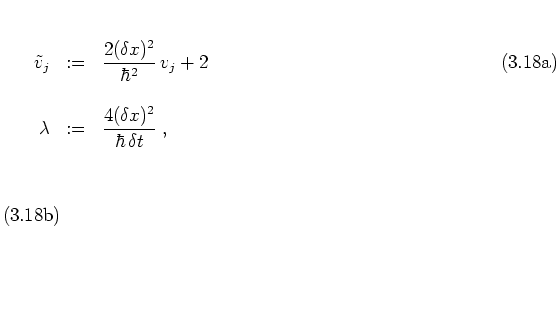
combination of
equations (3.16-3.18)
gives the
iteration scheme
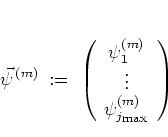 |
(3.20) |
 |
(3.21) |
The right hand side of equation (3.21)
is easily computed from the already known
![]() .
Then
.
Then
![]() is
determined by inversion of the (essentially) tridiagonal linear system
given by the matrix
is
determined by inversion of the (essentially) tridiagonal linear system
given by the matrix ![]() ;
for that purpose, several efficient algorithms are available
[PTVF94,Sto99].
;
for that purpose, several efficient algorithms are available
[PTVF94,Sto99].
As in the case of the TROTTER-based method, the time increment ![]() can be changed adaptively at each time step in order to control the
numerical accuracy of the algorithm. Also, as in the TROTTER algorithm, changing the spatial nodes (and thus
can be changed adaptively at each time step in order to control the
numerical accuracy of the algorithm. Also, as in the TROTTER algorithm, changing the spatial nodes (and thus ![]() ) in the course
of the calculation is much more difficult and prone to cause
additional numerical error.
) in the course
of the calculation is much more difficult and prone to cause
additional numerical error.
Regarding the initial choice of
the parameters
![]() and
and ![]() , it is
natural to choose these parameters small enough such that the smallest
oscillation
of interest
(both with respect to time and space) of the system can be
resolved. Furthermore, these
parameters can be chosen in
such a way that the errors induced by time and space discretization are
balanced
-- this interdependence is made plausible by equation
(3.19b) which shows that
reducing
, it is
natural to choose these parameters small enough such that the smallest
oscillation
of interest
(both with respect to time and space) of the system can be
resolved. Furthermore, these
parameters can be chosen in
such a way that the errors induced by time and space discretization are
balanced
-- this interdependence is made plausible by equation
(3.19b) which shows that
reducing ![]() leads to similar numerical problems as increasing
leads to similar numerical problems as increasing
![]() ;
more information on this issue can be
found in [KW96] and references therein.
;
more information on this issue can be
found in [KW96] and references therein.