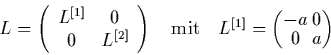Wir wenden uns zunächst der Frage nach der Zahl der Monome zu, aus
denen ein Quasiintegral
![]() zusammengesetzt ist.
zusammengesetzt ist.
Als Grundlage unserer Untersuchung dienen die drei magnetischen Flaschen,
für die wir in Kapitel 2 die Hamilton-Funktionen
hergeleitet haben: die Brown-Gabrielse-Magnetflasche (Gl. (3.1)), die Dragt-Finnsche ,,Mirror Machine`` (Gl. 2.41)) und das Størmer-System (Gl. (2.62)).
Um eine Vorstellung davon zu bekommen, inwieweit unsere Ergebnisse
spezifisch für Hamilton-Funktionen vom Magnetflaschentyp
(4.4) sind,
beziehen wir außerdem
das Hénon-Heiles-System [HeHe64] in unsere Betrachtungen ein.
Dieses System wird durch die folgende Hamilton-Funktion beschrieben:
| System | Zahl der Monome in |
||||
| Hénon-Heiles | Gustavson | 6 | -- $ $ | ,,einfach`` | |
| Brown-Gabrielse | Magnetflasche | 8 | -- $ $ | ,,einfach`` | |
| Dragt-Finn | Magnetflasche | 5 | -- $ $ | ,,einfach`` | |
| Størmer | Magnetflasche | 80 | -- $ $ | ,,kompliziert`` | |
Das Quasiintegral der Brown-Gabrielse-Magnetflasche entnehmen wir dem
Anhang D.
Mit unserem in Kapitel 4 beschriebenen Verfahren
-- das, weil es den Gustavson-Fall als Spezialfall enthält, auch auf
![]() anwendbar ist -- haben wir auch die anderen drei
Hamilton-Funktionen
auf DFS-Normalform transformiert und dann die entsprechenden
Quasiintegrale in den ursprünglichen Koordinaten bestimmt.
Wegen des trotz aller Vereinfachungen immer noch recht großen
Rechenaufwandes haben wir diese Transformationen nur bis zum Grad 12
einschließlich durchgeführt.
anwendbar ist -- haben wir auch die anderen drei
Hamilton-Funktionen
auf DFS-Normalform transformiert und dann die entsprechenden
Quasiintegrale in den ursprünglichen Koordinaten bestimmt.
Wegen des trotz aller Vereinfachungen immer noch recht großen
Rechenaufwandes haben wir diese Transformationen nur bis zum Grad 12
einschließlich durchgeführt.
Für die folgenden Untersuchungen stehen also die Quasiintegrale
![]() ,
,
![]() ,
,
![]() und
und
![]() mit
mit
![]() zur Verfügung.
Dabei ist zu beachten, daß die Hamilton-Funktionen
zur Verfügung.
Dabei ist zu beachten, daß die Hamilton-Funktionen
![]() sowie
sowie ![]() und somit auch die entsprechenden
Quasiintegrale gerade Funktionen sind.
und somit auch die entsprechenden
Quasiintegrale gerade Funktionen sind.
Wir geben die ![]() hier nicht explizit an. Statt dessen diskutieren
wir, wie die Anzahl der Summanden dieser Polynome mit zunehmendem
hier nicht explizit an. Statt dessen diskutieren
wir, wie die Anzahl der Summanden dieser Polynome mit zunehmendem ![]() anwächst. Hierzu definieren wir
anwächst. Hierzu definieren wir ![]() als die Anzahl der Monome des
Quasiintegrals
als die Anzahl der Monome des
Quasiintegrals ![]() und werten diese Funktion für unsere
Beispielsysteme aus. Das Ergebnis dieser Abzählaufgabe ist in Abbildung
5.1 dargestellt.
und werten diese Funktion für unsere
Beispielsysteme aus. Das Ergebnis dieser Abzählaufgabe ist in Abbildung
5.1 dargestellt.
Bei kleinen Graden ![]() besteht das Quasiintegral des Hénon-Heiles-Systems
offensichtlich aus mehr Summanden als die Integrale der anderen Systeme.
Diese Tatsache liegt darin begründet,
daß das formale Integral
der auf Normalform transformierten Hamilton-Funktion
besteht das Quasiintegral des Hénon-Heiles-Systems
offensichtlich aus mehr Summanden als die Integrale der anderen Systeme.
Diese Tatsache liegt darin begründet,
daß das formale Integral
der auf Normalform transformierten Hamilton-Funktion ![]() mehr
Terme enthält
als die formalen Integrale der anderen normalisierten Systeme: Es
besteht aus vier Summanden, gegenüber den nur zwei Summanden bei den
Magnetflaschen-Hamilton-Funktionen. Man vergleiche hierzu die Gln. (4.4) und (4.13).
Mit größer werdendem
mehr
Terme enthält
als die formalen Integrale der anderen normalisierten Systeme: Es
besteht aus vier Summanden, gegenüber den nur zwei Summanden bei den
Magnetflaschen-Hamilton-Funktionen. Man vergleiche hierzu die Gln. (4.4) und (4.13).
Mit größer werdendem ![]() ändert
sich das Bild, denn nun macht sich der Einfluß der vielen Terme der
Størmer-Hamilton-Funktion (2.62) bemerkbar.
Ohne diesen Punkt hier eingehender
diskutieren zu wollen, merken wir an, daß eine komplizierte
Hamilton-Funktion bei der Lösung der homologischen Gleichung
(1.66a) im Zuge der Normalformtransformation
komplizierte erzeugende Funktionen
ändert
sich das Bild, denn nun macht sich der Einfluß der vielen Terme der
Størmer-Hamilton-Funktion (2.62) bemerkbar.
Ohne diesen Punkt hier eingehender
diskutieren zu wollen, merken wir an, daß eine komplizierte
Hamilton-Funktion bei der Lösung der homologischen Gleichung
(1.66a) im Zuge der Normalformtransformation
komplizierte erzeugende Funktionen ![]() zur Folge hat.
Umgekehrt bedeutet dies nach der Rücktransformation auf die
ursprünglichen Koordinaten, daß das Quasiintegral
entsprechend kompliziert ist.
Man erkennt diesen Sachverhalt in Abbildung 5.1 daran, daß
zur Folge hat.
Umgekehrt bedeutet dies nach der Rücktransformation auf die
ursprünglichen Koordinaten, daß das Quasiintegral
entsprechend kompliziert ist.
Man erkennt diesen Sachverhalt in Abbildung 5.1 daran, daß
![]() bei wachsendem
bei wachsendem ![]() sehr schnell eine mit
sehr schnell eine mit
![]() vergleichbare Monomanzahl erreicht.
Dagegen besitzen die zu den einfacheren Hamilton-Funktionen
vergleichbare Monomanzahl erreicht.
Dagegen besitzen die zu den einfacheren Hamilton-Funktionen
![]() und
und ![]() gehörenden Quasiintegrale durchweg nur
etwa halb so viele Summanden wie die beiden anderen
gehörenden Quasiintegrale durchweg nur
etwa halb so viele Summanden wie die beiden anderen ![]() .
.
Interessant ist auch der Vergleich der Monomzahl der beiden Quasiintegrale
![]() und
und
![]() .
In Abschnitt 2.3 haben wir beschrieben, wie die
Dragt-Finn-Flasche als gezielte Vereinfachung der Brown-Gabrielse-Flasche
konstruiert wird. Die
einfachere Struktur von
.
In Abschnitt 2.3 haben wir beschrieben, wie die
Dragt-Finn-Flasche als gezielte Vereinfachung der Brown-Gabrielse-Flasche
konstruiert wird. Die
einfachere Struktur von ![]() gegenüber
gegenüber ![]() schlägt
sich tatsächlich in der Abbildung 5.1 nieder, aber der Effekt ist
eher marginal. Typischerweise ist die Monomzahl der Brown-Gabrielse-Flasche
nur um einen Faktor 1.2 bis 1.3 größer als die der Dragt-Finn-Flasche.
schlägt
sich tatsächlich in der Abbildung 5.1 nieder, aber der Effekt ist
eher marginal. Typischerweise ist die Monomzahl der Brown-Gabrielse-Flasche
nur um einen Faktor 1.2 bis 1.3 größer als die der Dragt-Finn-Flasche.
Wir können demnach feststellen, daß die Komplexität der zugrunde
liegenden Hamilton-Funktion die Komplexität des Quasiintegrals in der
Tat beeinflußt. Dieser Effekt wird aber erst bedeutsam, wenn man
zwei Hamilton-Funktionen vergleicht, deren Summandenzahlen sich sehr stark
unterscheiden, beispielsweise ![]() und
und ![]() .
Entscheidender ist der Einfluß der Gestalt des quadratischen Anteils der
Hamilton-Funktion. Wir haben gesehen, daß ein Gustavsonsches
.
Entscheidender ist der Einfluß der Gestalt des quadratischen Anteils der
Hamilton-Funktion. Wir haben gesehen, daß ein Gustavsonsches ![]() zu einem erheblich komplexeren Quasiintegral führt als ein
Magnetflaschen-
zu einem erheblich komplexeren Quasiintegral führt als ein
Magnetflaschen-![]() mit einer vergleichbaren Summandenzahl.
mit einer vergleichbaren Summandenzahl.
Es ist ein auffallendes Merkmal der Abbildung 5.1, daß
![]() für alle vier betrachteten Systeme bei hinreichend großem
für alle vier betrachteten Systeme bei hinreichend großem ![]() einem Potenzgesetz genügt. Offensichtlich gilt in sehr guter
Näherung:
einem Potenzgesetz genügt. Offensichtlich gilt in sehr guter
Näherung:
| (5.2) |
| System |
|
| Hénon-Heiles | 3.02 |
| Brown-Gabrielse | 3.11 |
| Dragt-Finn | 3.16 |
| Størmer | 3.25 |
| (5.3) |
Interessanterweise wächst in dem betrachteten ![]() -Intervall die
Dimension des Polynomraumes
-Intervall die
Dimension des Polynomraumes
 ,
dessen Elemente die
,
dessen Elemente die ![]() ja sind, nach fast genau dem gleichen
Potenzgesetz, denn es gilt:
ja sind, nach fast genau dem gleichen
Potenzgesetz, denn es gilt:
| (5.4) |