


Nächste Seite: Nachweis gebundener Bewegung
Aufwärts: Dynamik in der Brown-Gabrielse-Magnetflasche
Vorherige Seite: Dynamik in der Brown-Gabrielse-Magnetflasche
Inhalt
Das Potential 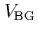
Die Hamilton-Funktion 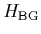 der Brown-Gabrielse-Magnetflasche
haben wir in Gl. (2.33) angegeben. Wir beschränken uns
im folgenden auf den in Abschnitt 2.2 diskutierten Fall
der Brown-Gabrielse-Magnetflasche
haben wir in Gl. (2.33) angegeben. Wir beschränken uns
im folgenden auf den in Abschnitt 2.2 diskutierten Fall
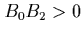 ; die Analyse des Falles
; die Analyse des Falles 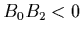 verliefe
vollständig analog zu den Untersuchungen des vorliegenden Kapitels. Die
im folgenden betrachtete Hamilton-Funktion lautet demnach:
verliefe
vollständig analog zu den Untersuchungen des vorliegenden Kapitels. Die
im folgenden betrachtete Hamilton-Funktion lautet demnach:
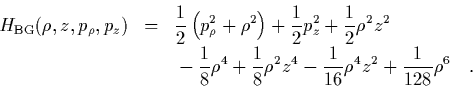 |
(3.1) |
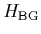 beschreibt ein Teilchen mit zwei Freiheitsgraden
der Bewegung.
Hierbei ist zu beachten, daß die Koordinate
beschreibt ein Teilchen mit zwei Freiheitsgraden
der Bewegung.
Hierbei ist zu beachten, daß die Koordinate 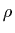 im Gegensatz zu
im Gegensatz zu 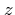 keine gewöhnliche
kartesische Koordinate ist, sondern den Abstand von der
keine gewöhnliche
kartesische Koordinate ist, sondern den Abstand von der 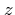 -Achse
bezeichnet.
Deshalb kann
-Achse
bezeichnet.
Deshalb kann 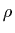 eigentlich nicht negativ werden.
Es ist aber trotzdem sinnvoll, negative
eigentlich nicht negativ werden.
Es ist aber trotzdem sinnvoll, negative 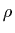 -Werte zuzulassen,
weil auch
-Werte zuzulassen,
weil auch 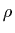 dann wie eine gewöhnliche kartesische Koordinate
behandelt werden kann.
dann wie eine gewöhnliche kartesische Koordinate
behandelt werden kann.
Um dieses Vorgehen zu verdeutlichen, betrachten wir eine Trajektorie, die
zur Zeit 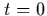 die
die 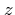 -Achse durchläuft:
-Achse durchläuft: 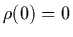 . Wegen der Wahl
. Wegen der Wahl
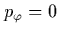 in Gl. (2.28) sind solche Trajektorien möglich,
denn nur im Fall
in Gl. (2.28) sind solche Trajektorien möglich,
denn nur im Fall
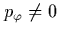 verhindert der Term
verhindert der Term
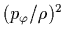 in der Hamilton-Funktion (2.16) das Erreichen der
in der Hamilton-Funktion (2.16) das Erreichen der
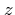 -Achse. Wir untersuchen, wie sich der Winkel
-Achse. Wir untersuchen, wie sich der Winkel 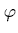 mit der Zeit
ändert. Zunächst folgt, unter Berücksichtigung der Gln. (2.21,2.25,2.11) und von
Tabelle 2.1,
mit der Zeit
ändert. Zunächst folgt, unter Berücksichtigung der Gln. (2.21,2.25,2.11) und von
Tabelle 2.1,
somit ist 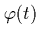 für
für 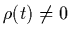 stetig. Für
stetig. Für
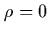 ist
ist 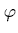 aber nicht definiert. Hier sind zwei Fälle zu
unterscheiden: Entweder ist
aber nicht definiert. Hier sind zwei Fälle zu
unterscheiden: Entweder ist
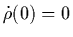 , dann bleibt das Teilchen
für alle Zeiten auf der
, dann bleibt das Teilchen
für alle Zeiten auf der 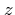 -Achse und bewegt sich frei, weil in der
Hamilton-Funktion alle Terme bis auf
-Achse und bewegt sich frei, weil in der
Hamilton-Funktion alle Terme bis auf
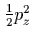 verschwinden.
Oder aber es gilt
verschwinden.
Oder aber es gilt
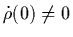 . Dann schneidet das Teilchen die
. Dann schneidet das Teilchen die
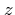 -Achse, und
-Achse, und 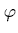 macht einen Sprung um
macht einen Sprung um 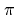 , ist also nicht
stetig in
, ist also nicht
stetig in 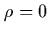 . Diesem
,,Durchpendeln`` durch die
. Diesem
,,Durchpendeln`` durch die 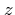 -Achse tragen wir dadurch Rechnung, daß
wir negative
-Achse tragen wir dadurch Rechnung, daß
wir negative 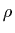 -Werte zulassen.
In Abbildung 3.1 veranschaulichen wir diese
Verallgemeinerung von
-Werte zulassen.
In Abbildung 3.1 veranschaulichen wir diese
Verallgemeinerung von 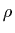 .
Damit können wir
.
Damit können wir 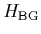 als die Hamilton-Funktion eines Systems mit zwei Freiheitsgraden der
Bewegung in
als die Hamilton-Funktion eines Systems mit zwei Freiheitsgraden der
Bewegung in 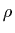 - und
- und 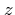 -Richtung ansehen, bei dem die Koordinate
-Richtung ansehen, bei dem die Koordinate
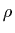 keinen besonderen Beschränkungen mehr unterliegt.
keinen besonderen Beschränkungen mehr unterliegt.
Wir zerlegen die Hamilton-Funktion (2.33) in die Summe
ihres kinetischen Anteils und eines Potentials
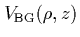 ,
,
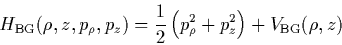 |
(3.2) |
mit
und wenden uns im folgenden der Untersuchung dieses Potentials zu.
Abbildung 3.2 zeigt die Äquipotentiallinien von
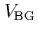 .
.
Das Potential ist positiv semidefinit. Die Berechnung der kritischen
Punkte von 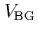 durch Nullsetzen des Gradienten
durch Nullsetzen des Gradienten
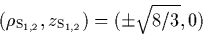 |
(3.4) |
ergibt zwei Sattelpunkte
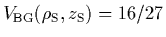 mit der Potentialhöhe
mit der Potentialhöhe
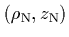 . Außerdem sind auch
die Punkte
. Außerdem sind auch
die Punkte
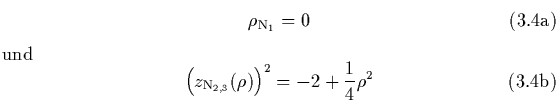 der drei durch
der drei durch
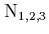
beschriebenen Kurven kritische Punkte; auf diesen drei eindimensionalen
Mannigfaltigkeiten hat das Potential den Wert null.
Wir untersuchen zunächst, inwiefern die Bezeichnung des durch Gl. (3.1)
beschriebenen Systems als magnetische ,,Flasche`` gerechtfertigt ist.
Unterabschnitte



Nächste Seite: Nachweis gebundener Bewegung
Aufwärts: Dynamik in der Brown-Gabrielse-Magnetflasche
Vorherige Seite: Dynamik in der Brown-Gabrielse-Magnetflasche
Inhalt
Martin_Engel
2000-05-25
![]() der Brown-Gabrielse-Magnetflasche
haben wir in Gl. (2.33) angegeben. Wir beschränken uns
im folgenden auf den in Abschnitt 2.2 diskutierten Fall
der Brown-Gabrielse-Magnetflasche
haben wir in Gl. (2.33) angegeben. Wir beschränken uns
im folgenden auf den in Abschnitt 2.2 diskutierten Fall
![]() ; die Analyse des Falles
; die Analyse des Falles ![]() verliefe
vollständig analog zu den Untersuchungen des vorliegenden Kapitels. Die
im folgenden betrachtete Hamilton-Funktion lautet demnach:
verliefe
vollständig analog zu den Untersuchungen des vorliegenden Kapitels. Die
im folgenden betrachtete Hamilton-Funktion lautet demnach:
![]() die
die ![]() -Achse durchläuft:
-Achse durchläuft: ![]() . Wegen der Wahl
. Wegen der Wahl
![]() in Gl. (2.28) sind solche Trajektorien möglich,
denn nur im Fall
in Gl. (2.28) sind solche Trajektorien möglich,
denn nur im Fall
![]() verhindert der Term
verhindert der Term
![]() in der Hamilton-Funktion (2.16) das Erreichen der
in der Hamilton-Funktion (2.16) das Erreichen der
![]() -Achse. Wir untersuchen, wie sich der Winkel
-Achse. Wir untersuchen, wie sich der Winkel ![]() mit der Zeit
ändert. Zunächst folgt, unter Berücksichtigung der Gln. (2.21,2.25,2.11) und von
Tabelle 2.1,
mit der Zeit
ändert. Zunächst folgt, unter Berücksichtigung der Gln. (2.21,2.25,2.11) und von
Tabelle 2.1,
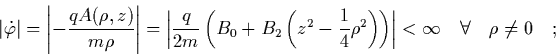
![]() ,
,
![]() .
.
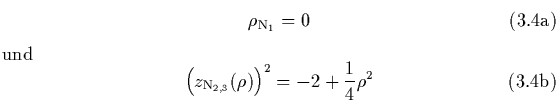 der drei durch
der drei durch