|
Our interpretation of the experimental material rests
essentially on the classical concepts.
NIELS BOHR |
In this appendix I present
a number of
typical examples of
quantum stochastic webs and localized quantum dynamics
that are generated by the quantum map (2.37).
See section 3.3 for a more detailed description of how
the quantum states
![]() shown in these pictures are generated.
In chapters 4 and
5 some important aspects of the quantum
dynamics leading to these
shown in these pictures are generated.
In chapters 4 and
5 some important aspects of the quantum
dynamics leading to these
![]() are described and explained.
are described and explained.
Having studied the dynamics for several different initial states
![]() it has turned out that
in the resonance cases (1.33)
essentially there are just two important types of
it has turned out that
in the resonance cases (1.33)
essentially there are just two important types of
![]() : those
located in quantum phase space in one of the meshes of the
classical stochastic web,
and those centered
in a stochastic region of the classical web, i.e. in a channel of
the web. All other initial states are combinations of these two types,
and regardless of the actual position of the ``initial mesh'' or
``initial channel''
chosen for
: those
located in quantum phase space in one of the meshes of the
classical stochastic web,
and those centered
in a stochastic region of the classical web, i.e. in a channel of
the web. All other initial states are combinations of these two types,
and regardless of the actual position of the ``initial mesh'' or
``initial channel''
chosen for
![]() ,
the dynamics yield
comparable results.
Therefore, in the following sections two types of initial states are
considered:
states centered around the origin
,
the dynamics yield
comparable results.
Therefore, in the following sections two types of initial states are
considered:
states centered around the origin ![]() of phase space,
i.e. in a mesh,
and states centered around one of those intersections of
stochastic channels
that are closest to the origin,
at
of phase space,
i.e. in a mesh,
and states centered around one of those intersections of
stochastic channels
that are closest to the origin,
at ![]() with suitable
with suitable ![]() .
.
For better comparison, depending on the value of ![]() ,
harmonic oscillator eigenstates
,
harmonic oscillator eigenstates
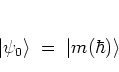 |
(C.1) |
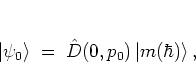 |
(C.3) |
In chapter 3 I have
discussed
the way in which
the size
![]() of the basis
of the basis
![]() used
for expanding the quantum states affects the accuracy of the algorithm.
Only the phase space region
used
for expanding the quantum states affects the accuracy of the algorithm.
Only the phase space region
![\begin{displaymath}
\left\{
(x,p)^t \; \bigg\vert \
\sqrt{x^2+p^2} \; { {\prot...
...iptsize max}}+1)
\rule[-0.1cm]{0.0cm}{0.42cm}
} \,
\right\}
\end{displaymath}](img1553.png) |
(C.4) |
|
For the series of figures shown below, the parameters ![]() and
and ![]() are varied more or less systematically in order to yield
states which are as prototypical as possible.
The states
are varied more or less systematically in order to yield
states which are as prototypical as possible.
The states
![]() obtained in this way are then converted into
their corresponding HUSIMI distributions
(cf. appendix A).
The lines
in the following contour plots of HUSIMI distributions
are drawn at 10%, 20%, ..., 90%, 99%
of the respective maximum values of
obtained in this way are then converted into
their corresponding HUSIMI distributions
(cf. appendix A).
The lines
in the following contour plots of HUSIMI distributions
are drawn at 10%, 20%, ..., 90%, 99%
of the respective maximum values of
![]() for each
state
for each
state
![]() .
.