Die wesentliche Motivation zur Einführung der Gustavson-Normalform
war die Suche nach einem weiteren Integral der Bewegung, das man sich
in der Tat mit der Gustavsonschen Theorie in Gestalt von
![]() verschaffen konnte.
Mit
verschaffen konnte.
Mit
![]() ist hier der quadratische Anteil der
durch die Transformation
ist hier der quadratische Anteil der
durch die Transformation
![]() auf Normalform
gebrachten Hamilton-Funktion gemeint.
In [Gu66] wird gezeigt, daß eine
Hamilton-Funktion mit einem quadratischen Anteil vom Gustavson-Typ
(1.61) über
auf Normalform
gebrachten Hamilton-Funktion gemeint.
In [Gu66] wird gezeigt, daß eine
Hamilton-Funktion mit einem quadratischen Anteil vom Gustavson-Typ
(1.61) über
![]() hinaus noch
weitere unabhängige Integrale der
Bewegung1.9besitzen kann.
hinaus noch
weitere unabhängige Integrale der
Bewegung1.9besitzen kann.
Genauer gilt folgende Aussage: Wir betrachten eine Hamilton-Funktion, die
in Gustavson-Normalform ist und deren Frequenzen ![]() in
in
![]() -facher Resonanz sind, mit
-facher Resonanz sind, mit ![]() . Das heißt, die
Frequenzen genügen
. Das heißt, die
Frequenzen genügen ![]() linear unabhängigen
Kommensurabilitätsbedingungen
linear unabhängigen
Kommensurabilitätsbedingungen
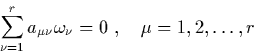 |
(1.74) |
| (1.75) |
![[*]](crossref.png) .
.
Diese Aussage ist
eine direkte Folge der Tatsache, daß
![]() in Gustavson-Normalform ist: Zum Beweis untersucht man den
Ausdruck
in Gustavson-Normalform ist: Zum Beweis untersucht man den
Ausdruck
![]() in den
,,diagonalisierenden`` Phasenraumkoordinaten
in den
,,diagonalisierenden`` Phasenraumkoordinaten
![]() aus Gl. (1.73). Es zeigt sich dann sofort, daß diese
Poisson-Klammer genau dann verschwindet, wenn die
aus Gl. (1.73). Es zeigt sich dann sofort, daß diese
Poisson-Klammer genau dann verschwindet, wenn die
![]() der Bedingung (1.103) genügen.
der Bedingung (1.103) genügen.
Für eine Hamilton-Funktion in DFS-Normalform stellt sich die Situation
nicht mehr so überschaubar dar. In Analogie zur Gustavsonschen Theorie
liegt es nahe zu vermuten, daß ![]() , welches in der DFS-Theorie die
Rolle von
, welches in der DFS-Theorie die
Rolle von ![]() übernimmt, ein Integral der Bewegung sei. Dies gilt aber
nicht, denn es ist
übernimmt, ein Integral der Bewegung sei. Dies gilt aber
nicht, denn es ist
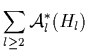 |
|||
| (1.78) |
Bei der Untersuchung von sogenannten magnetischen Flaschen (vgl. Kapitel
2) sind Hamilton-Funktionen mit
Über die speziellen, von Gustavson (Gl. (1.61)) bzw. Dragt und Finn (Gl. (1.105)) betrachteten
Hamilton-Funktionen hinaus gibt es weitere
Funktionen in
![]() , die als quadratische Anteile
, die als quadratische Anteile
![]() von Potenzreihen-Hamilton-Funktionen auftreten
können1.10.
Die Verallgemeinerung des Dragt-Finnschen Resultates auf ein beliebiges
dieser
von Potenzreihen-Hamilton-Funktionen auftreten
können1.10.
Die Verallgemeinerung des Dragt-Finnschen Resultates auf ein beliebiges
dieser
![]() gelingt
mit Hilfe einer geeigneten Zerlegung von
gelingt
mit Hilfe einer geeigneten Zerlegung von ![]() . Wir gehen von der
allgemein gültigen Darstellung (1.95) des quadratischen
Anteils der Hamilton-Funktion aus:
. Wir gehen von der
allgemein gültigen Darstellung (1.95) des quadratischen
Anteils der Hamilton-Funktion aus:
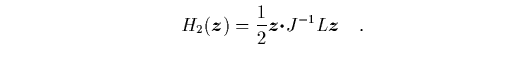
![]()
![]() und damit auch
und damit auch ![]() werden durch die
werden durch die
![]() -Matrix
-Matrix ![]() eindeutig festgelegt. Wir spalten
eindeutig festgelegt. Wir spalten ![]() mit Hilfe der
Jordan-Chevalley-Zerlegung [Hu87] in einen
(über
mit Hilfe der
Jordan-Chevalley-Zerlegung [Hu87] in einen
(über ![]() )
diagonalisierbaren Anteil
)
diagonalisierbaren Anteil ![]() und einen nilpotenten Anteil
und einen nilpotenten Anteil ![]() auf:
auf:
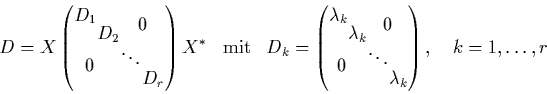
![\begin{displaymath}
N = X \left( \begin{array}{@{}c@{}c@{}}
\begin{array}{@{}c...
...]
0 & \cdots & & 0
\end{array} \right)
, \quad k=1,\ldots,r
\end{displaymath}](img432.png)
In Anhang A benutzen wir die Galinsche
Klassifizierung der quadratischen Hamilton-Funktionen, um für (fast) alle
Hamilton-Funktionen aus ![]() die entsprechenden Integrale
die entsprechenden Integrale ![]() zu bestimmen.
zu bestimmen.
An dieser Stelle zeigt sich noch einmal ein Charakteristikum der
Normalformentheorie: Es werden Aussagen über Elemente des
hochdimensionalen Vektorraumes ![]() gemacht, wobei vor allem
Eigenschaften des im Vergleich zu
gemacht, wobei vor allem
Eigenschaften des im Vergleich zu ![]() niedrigdimensionalen
niedrigdimensionalen
![]() in die Argumentation eingehen. Konkret heißt dies
bei der Bestimmung von Integralen der Bewegung, daß lediglich die
Jordan-Chevalley-Zerlegung einer
in die Argumentation eingehen. Konkret heißt dies
bei der Bestimmung von Integralen der Bewegung, daß lediglich die
Jordan-Chevalley-Zerlegung einer ![]() -Matrix gefunden werden muß,
um aus der in Normalform befindlichen Hamilton-Funktion ein Integral
der Bewegung zu bestimmen, dessen Grad
-Matrix gefunden werden muß,
um aus der in Normalform befindlichen Hamilton-Funktion ein Integral
der Bewegung zu bestimmen, dessen Grad ![]() -Anteile Elemente des
-Anteile Elemente des
![]() -dimensionalen Raumes
-dimensionalen Raumes ![]() sind.
Eine entsprechende Eigenschaft macht man sich auch bei der Transformation
auf Normalform zunutze: Um den Grad, bis zu dem sich die Hamilton-Funktion
in Normalform befindet, um eins zu erhöhen, muß man Elemente des
hochdimensionalen Vektorraumes
sind.
Eine entsprechende Eigenschaft macht man sich auch bei der Transformation
auf Normalform zunutze: Um den Grad, bis zu dem sich die Hamilton-Funktion
in Normalform befindet, um eins zu erhöhen, muß man Elemente des
hochdimensionalen Vektorraumes ![]() manipulieren. Diese Aufgabe wird
dadurch vereinfacht, daß die wesentlichen Gleichungen
(1.91) und (1.93) Strukturen (von
manipulieren. Diese Aufgabe wird
dadurch vereinfacht, daß die wesentlichen Gleichungen
(1.91) und (1.93) Strukturen (von ![]() bzw.
bzw. ![]() ) in dem nur
) in dem nur ![]() -dimensionalen Vektorraum
-dimensionalen Vektorraum ![]() betreffen.
betreffen.
Ein
zweiter wichtiger Punkt, der an dieser Stelle nicht außer acht
gelassen werden darf, ist die Tatsache, daß sowohl
![]() als auch
als auch
![]() lediglich formale Integrale
der Bewegung darstellen.
Zwar kann man jede
Hamilton-Funktion in Potenzreihengestalt in DFS-Normalform überführen,
indem man Grad für Grad homologische Gleichungen löst und entsprechend
Lie-transformiert. Daß aber das Resultat dieser sukzessiven
Transformationen für
lediglich formale Integrale
der Bewegung darstellen.
Zwar kann man jede
Hamilton-Funktion in Potenzreihengestalt in DFS-Normalform überführen,
indem man Grad für Grad homologische Gleichungen löst und entsprechend
Lie-transformiert. Daß aber das Resultat dieser sukzessiven
Transformationen für ![]() konvergiert, ist keineswegs
sichergestellt.
Beispielsweise kann
im Falle eines nichtintegrablen Systems mit zwei
Freiheitsgraden der Bewegung die Normalform-Transformation
nicht konvergieren, weil man sonst ein zweites Integral
der Bewegung erhielte. Dessen Existenz ist aber für ein nichtintegrables
System gerade ausgeschlossen.
konvergiert, ist keineswegs
sichergestellt.
Beispielsweise kann
im Falle eines nichtintegrablen Systems mit zwei
Freiheitsgraden der Bewegung die Normalform-Transformation
nicht konvergieren, weil man sonst ein zweites Integral
der Bewegung erhielte. Dessen Existenz ist aber für ein nichtintegrables
System gerade ausgeschlossen.
Wir gehen an dieser Stelle noch auf den Begriff des Quasiintegrals
ein. Selbst in dem Fall, daß die Transformation der Hamilton-Funktion
auf Normalform konvergiert, werden wir in der Praxis die Berechnung der
Normalform und damit auch des Integrals bei einem endlichen Grad ![]() abbrechen, weil die homologische Gleichung für jeden Grad neu gelöst
werden muß und man in der Regel kein allgemeines, für alle
abbrechen, weil die homologische Gleichung für jeden Grad neu gelöst
werden muß und man in der Regel kein allgemeines, für alle ![]() gültiges Transformationsgesetz findet. Deshalb erhalten wir nur eine
Approximation
gültiges Transformationsgesetz findet. Deshalb erhalten wir nur eine
Approximation
![]() ,
,
| (1.83) |
| (1.84) |
| (1.85) |
Gl. (1.112) verdeutlicht,
daß das formale Integral
![]() bzw. die
entsprechenden Quasiintegrale
bzw. die
entsprechenden Quasiintegrale
![]() im
allgemeinen eine sehr komplizierte algebraische Struktur aufweisen,
im Gegensatz zur Darstellung (1.108) des Integrals
als quadratisches Polynom in den Koordinaten
im
allgemeinen eine sehr komplizierte algebraische Struktur aufweisen,
im Gegensatz zur Darstellung (1.108) des Integrals
als quadratisches Polynom in den Koordinaten
![]() . Diese
Komplizierung ist bedingt durch die (unendlich vielen) bei der
Rücktransformation benötigten Lie-Transformationen
. Diese
Komplizierung ist bedingt durch die (unendlich vielen) bei der
Rücktransformation benötigten Lie-Transformationen
![]() .
.
Bei der Berechnung von Quasiintegralen für konkrete Beispielsysteme
-- in den Kapiteln 4 und 5
-- wird sich zeigen, daß die Oszillation des Quasiintegrals aufgrund
des Fehlerterms
![]() in Gl. (1.112)
schon für kleine Werte von
in Gl. (1.112)
schon für kleine Werte von ![]() unbedeutend werden kann.
Andererseits ist es auch möglich, daß der Fehlerterm selbst für kleine
unbedeutend werden kann.
Andererseits ist es auch möglich, daß der Fehlerterm selbst für kleine
![]() und größere
und größere ![]() dominiert und
dominiert und
![]() somit nicht annähernd konstant wird. Welcher
dieser Fälle eintritt, hängt von der Chaotizität des relevanten
Gebietes des Phasenraumes ab. Wir werden uns diesem Problem in Kapitel
4 zuwenden.
somit nicht annähernd konstant wird. Welcher
dieser Fälle eintritt, hängt von der Chaotizität des relevanten
Gebietes des Phasenraumes ab. Wir werden uns diesem Problem in Kapitel
4 zuwenden.
Selbst im Fall der Nichtkonvergenz der Normalformtransformation stellen aber die niedrigsten Terme der Normalform in der Regel ein sehr nützliches Hilfsmittel zur Analyse des Phasenportraits dar und ermöglichen die Untersuchung von periodischen Orbits, invarianten Tori und deren Bifurkationen [ShRe82,Ro84].