Der in Abschnitt 1.2.2 beschriebene Normalformenkalkül
ist nur auf Hamilton-Funktionen anwendbar, deren quadratischer Anteil
die Gestalt (1.61) hat.
Den Grund für diese Einschränkung
machen wir uns an einem einfachen Beispiel klar. Wir betrachten ein
Teilchen mit einem Freiheitsgrad der Bewegung (![]() ), das sich in
niedrigster Ordnung frei bewegt:
), das sich in
niedrigster Ordnung frei bewegt:
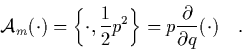 |
(1.61) |
![\begin{displaymath}
\quad
\begin{array}{lcl}
{\cal A}_3 (p^3) & = & 0 \\ [0.2...
...2q \\ [0.2cm]
{\cal A}_3 (q^3) & = & 3pq^2 \quad,
\end{array}\end{displaymath}](img337.png) |
(1.62) |
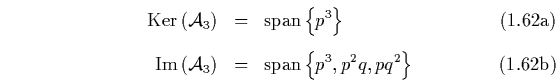
| (1.62) |
Für beliebige quadratische Terme der Hamilton-Funktion ist also die Gültigkeit der Zerlegung (1.68) keineswegs sichergestellt. Aber nur wegen dieser Zerlegung ist die Definition der Gustavson-Normalform sinnvoll, denn erst Gl. (1.68) ermöglicht die Lösung der homologischen Gleichung (1.66a) und damit die Durchführung einer normalisierenden Transformation.
Vor diesem Hintergrund benötigen wir also eine von ![]() erzeugte
Zerlegung
von
erzeugte
Zerlegung
von ![]() , die für alle
, die für alle ![]() , das heißt für alle möglichen
quadratischen Anteile
, das heißt für alle möglichen
quadratischen Anteile ![]() der Hamilton-Funktion gültig ist.
Die für die Lösung dieser Frage entscheidende Idee wird in
[DrFi79] beschrieben:
Wir betrachten einen endlich-dimensionalen unitären Vektorraum
der Hamilton-Funktion gültig ist.
Die für die Lösung dieser Frage entscheidende Idee wird in
[DrFi79] beschrieben:
Wir betrachten einen endlich-dimensionalen unitären Vektorraum ![]() mit
dem Skalarprodukt
mit
dem Skalarprodukt
![]() . Zu jedem linearen Operator
. Zu jedem linearen Operator ![]() auf
auf ![]() ist über
ist über
![]() der entsprechende adjungierte Operator
der entsprechende adjungierte Operator ![]() definiert.
Die aus der linearen Algebra bekannte Fredholmsche Alternative
[MeHa92]
besagt, daß dann
definiert.
Die aus der linearen Algebra bekannte Fredholmsche Alternative
[MeHa92]
besagt, daß dann
| (1.63) |
Mit dieser Zerlegung von ![]() können wir nun ein erweitertes
Normalformenkonzept einführen.
können wir nun ein erweitertes
Normalformenkonzept einführen.
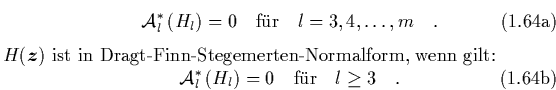
Ein wichtiger Unterschied zwischen dieser Definition und derjenigen
der Gustavson-Normalform, Gl. (1.62), besteht darin,
daß Gl. (1.89)
nicht für ![]() erfüllt sein muß und es im allgemeinen auch nicht ist.
erfüllt sein muß und es im allgemeinen auch nicht ist.
![]() auf Normalform gemäß Gl. (1.89) zu
transformieren, z. B. mittels einer Lie-Transformation, wäre sinnlos,
denn mit einer Änderung von
auf Normalform gemäß Gl. (1.89) zu
transformieren, z. B. mittels einer Lie-Transformation, wäre sinnlos,
denn mit einer Änderung von ![]() änderte sich auch der Operator
änderte sich auch der Operator
![]() !
Dagegen ist die entsprechende Gleichung im Gustavsonschen Fall
für
!
Dagegen ist die entsprechende Gleichung im Gustavsonschen Fall
für ![]() immer erfüllt.
Dies ist im Rahmen der Gustavsonschen Theorie auch
notwendig, damit
immer erfüllt.
Dies ist im Rahmen der Gustavsonschen Theorie auch
notwendig, damit ![]() ein Integral der Bewegung ist. Dieser Unterschied
zwischen den beiden diskutierten Normalformbegriffen wird im folgenden
Abschnitt 1.2.4 eine wichtige Rolle spielen.
Dort werden wir zeigen, wie man auch für eine Hamilton-Funktion in
DFS-Normalform ein Integral der Bewegung angeben kann, in Analogie
zum Integral
ein Integral der Bewegung ist. Dieser Unterschied
zwischen den beiden diskutierten Normalformbegriffen wird im folgenden
Abschnitt 1.2.4 eine wichtige Rolle spielen.
Dort werden wir zeigen, wie man auch für eine Hamilton-Funktion in
DFS-Normalform ein Integral der Bewegung angeben kann, in Analogie
zum Integral ![]() der Gustavson-Theorie.
der Gustavson-Theorie.
Die Definition 1.4 ist in dieser Allgemeinheit noch
nicht praktisch anwendbar. Es bleibt noch, ein geeignetes Skalarprodukt
auf den Räumen ![]() zu spezifizieren, mit dessen Hilfe
zu spezifizieren, mit dessen Hilfe ![]() definiert und explizit angegeben werden kann. Diese Wahl kann nach
Gesichtspunkten der Zweckmäßigkeit geschehen, man unterliegt dabei
keinen weiteren Einschränkungen.
Das folgende Skalarprodukt [Ba61] erweist sich dabei als
besonders nützlich.
Es wurde von Elphick et al. [ElEA87] in die Normalformentheorie
eingebracht und von Stegemerten, Meyer und Hall [St91,MeHa92]
wieder
aufgegriffen1.8.
definiert und explizit angegeben werden kann. Diese Wahl kann nach
Gesichtspunkten der Zweckmäßigkeit geschehen, man unterliegt dabei
keinen weiteren Einschränkungen.
Das folgende Skalarprodukt [Ba61] erweist sich dabei als
besonders nützlich.
Es wurde von Elphick et al. [ElEA87] in die Normalformentheorie
eingebracht und von Stegemerten, Meyer und Hall [St91,MeHa92]
wieder
aufgegriffen1.8.
Für ein Polynom
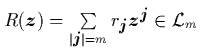 mit
mit
![]() und ein entsprechend definiertes Polynom
und ein entsprechend definiertes Polynom
![]() setzen wir
setzen wir
Im folgenden wollen wir ![]() und
und ![]() in einer einfach zu
benutzenden Form darstellen. Zunächst betrachten wir
in einer einfach zu
benutzenden Form darstellen. Zunächst betrachten wir ![]() und
benutzen die Darstellung (1.46b) der Poisson-Klammer
sowie die Definition (1.33) der Hamilton-Matrix:
und
benutzen die Darstellung (1.46b) der Poisson-Klammer
sowie die Definition (1.33) der Hamilton-Matrix:
Eine analoge Darstellung von ![]() zu finden, ist etwas aufwendiger.
Wir beginnen mit der Definition des zu
zu finden, ist etwas aufwendiger.
Wir beginnen mit der Definition des zu ![]() adjungierten Operators,
adjungierten Operators,
| (1.66) |
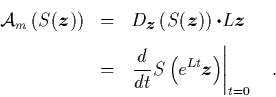
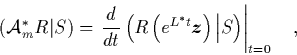
Wir kehren kurz zu dem Beispiel vom Anfang dieses
Abschnitts
zurück und
demonstrieren die Gültigkeit der Zerlegung (1.88)
im Fall ![]() für das
für das ![]() der Gl. (1.82).
der Gl. (1.82). ![]() ergibt sich zu
ergibt sich zu
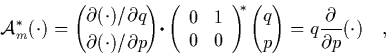
Es stellt sich natürlich die Frage, ob auch ![]() ein zu irgendeinem
Polynom
ein zu irgendeinem
Polynom ![]() adjungierter Lie-Operator ist. Man überzeugt
sich durch Nachrechnen leicht davon, daß dies für
adjungierter Lie-Operator ist. Man überzeugt
sich durch Nachrechnen leicht davon, daß dies für
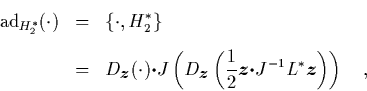
Man beachte auch hier die Ähnlichkeit von ![]() in Gl. (1.94) und des entsprechenden Ausdrucks für den
quadratischen Anteil der Hamilton-Funktion:
in Gl. (1.94) und des entsprechenden Ausdrucks für den
quadratischen Anteil der Hamilton-Funktion:
Nachdem wir uns die benötigten Hilfsmittel verschafft haben, können wir eine zu Gustavsons Satz analoge Aussage machen:
![]()
![]()
und statt der ![]() -Zerlegung (1.68) deren
Entsprechung (1.88) zu verwenden.
Unabhängig von Stegemerten wurde Satz 1.3 auch in
[MeHa92] bewiesen.
-Zerlegung (1.68) deren
Entsprechung (1.88) zu verwenden.
Unabhängig von Stegemerten wurde Satz 1.3 auch in
[MeHa92] bewiesen.
Wir gehen an dieser Stelle noch kurz auf den Zusammenhang zwischen der
Gustavsonschen und der DFS-Normalform ein.
Für ein ![]() vom Gustavson-Typ (1.61) ist
vom Gustavson-Typ (1.61) ist
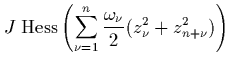 |
|||
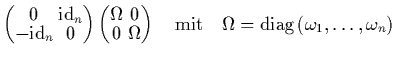 |
|||
![$\displaystyle \left(\protect\begin{array}{@{}c@{\hspace*{0.1cm}}
c@{}}0&\Omega\\ [-0.1cm]-\Omega&0\protect\end{array}\right) \quad,$](img389.png) |
(1.70) |
| (1.71) |
| (1.72) | |||
| (1.73) |
Im folgenden Abschnitt zeigen wir, daß die Normalformentheorie für Hamilton-Systeme physikalisch relevant ist: Die wichtigste Anwendung dieser Theorie ist die Konstruktion von Integralen der Bewegung.