


Nächste Seite: Die Birkhoff-Gustavson-Normalform
Aufwärts: Normalformen und Quasiintegrale für
Vorherige Seite: Normalformen und Quasiintegrale für
Inhalt
Lie-Transformationen
Wir betrachten ein autonomes Hamilton-System (1.1) mit
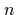 Freiheitsgraden der Bewegung. Die Hamilton-Funktion
Freiheitsgraden der Bewegung. Die Hamilton-Funktion
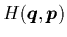 liege in Form einer formalen Potenzreihe
vor und habe nur Summanden
mit einem (Total-) Grad, der mindestens 2 ist. Wir berücksichtigen also
nur solche Systeme, die einen Fixpunkt haben und legen diesen, ohne
Beschränkung der
Allgemeinheit1.4,
in den Ursprung.
liege in Form einer formalen Potenzreihe
vor und habe nur Summanden
mit einem (Total-) Grad, der mindestens 2 ist. Wir berücksichtigen also
nur solche Systeme, die einen Fixpunkt haben und legen diesen, ohne
Beschränkung der
Allgemeinheit1.4,
in den Ursprung.
Um eine kompaktere Notation zu erreichen, benutzen wir, ebenso wie in
Abschnitt 1.1.2, den 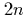 -Vektor
-Vektor
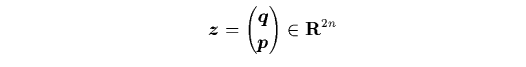
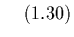
und können damit für die Hamilton-Funktion schreiben:
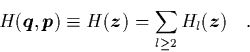 |
(1.31) |
Die 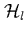 sind homogene Polynome vom Grad
sind homogene Polynome vom Grad 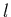 in den Phasenraumkoordinaten
in den Phasenraumkoordinaten
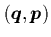 bzw.
bzw.
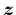 :
:
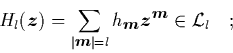 |
(1.32) |
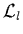 bezeichnet den Vektorraum der homogenen Polynome vom Grad
bezeichnet den Vektorraum der homogenen Polynome vom Grad 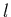 in
in
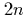 Variablen.
Die Dimension dieses Vektorraumes ist um den Faktor
Variablen.
Die Dimension dieses Vektorraumes ist um den Faktor 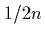 kleiner als die
seines Pendants
kleiner als die
seines Pendants 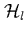 , was dadurch bedingt ist, daß die Elemente von
, was dadurch bedingt ist, daß die Elemente von
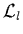 skalare Polynome sind, im Gegensatz zu den
vektorwertigen Polynomen in
skalare Polynome sind, im Gegensatz zu den
vektorwertigen Polynomen in 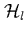 .
Da die Polynomräume
.
Da die Polynomräume 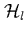 und
und 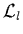 für größere Grade
für größere Grade 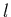 sehr
hochdimensional werden [PlEA78],
sehr
hochdimensional werden [PlEA78],
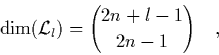 |
(1.33) |
erweist sich die Reduktion der Dimension beim Übergang von 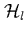 zu
zu
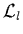 bei praktischen Berechnungen als sehr nützlich: In
Kapitel 4 werden beispielsweise Polynome vom Grad
14 betrachtet, was bei
bei praktischen Berechnungen als sehr nützlich: In
Kapitel 4 werden beispielsweise Polynome vom Grad
14 betrachtet, was bei 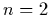 auf
auf
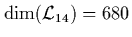 führt.
führt.
Wir definieren noch den (unendlichdimensionalen) Vektorraum aller
formalen Potenzreihen als die direkte Summe der 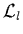 :
:
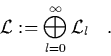 |
(1.34) |
Analog zu der Vorgehensweise in Abschnitt 1.1.1 diskutieren
wir zunächst eine wichtige Klasse von Transformationen, die das
wesentliche Hilfsmittel für die Darstellung der Normalformentheorie und
die Durchführung der Transformation einer Hamilton-Funktion auf
Normalform sind.
Dabei stützen wir uns vor allem auf die Darstellung in
[DrFi76a,DrFi79].
Wir beginnen mit der
Definition 1.1
:
Der zu
der Potenzreihe
adjungierte Lie-Operator ist
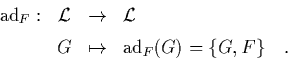 |
(1.35) |
 symbolisiert hierbei die Poisson-Klammer:
symbolisiert hierbei die Poisson-Klammer:
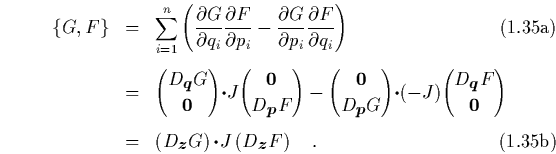
Speziell für den Lie-Operator, der zum quadratischen Anteil 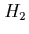 der
Hamilton-Funktion adjungiert ist, setzen wir
der
Hamilton-Funktion adjungiert ist, setzen wir
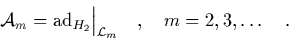 |
(1.35) |
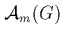 steht also für die Poisson-Klammer des Grad
steht also für die Poisson-Klammer des Grad 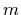 -Polynoms
-Polynoms
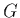 mit
mit 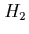 . Wichtig ist die Invarianz von
. Wichtig ist die Invarianz von 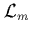 unter
unter 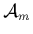 :
Für
:
Für 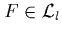 und
und 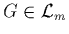 ist
ist
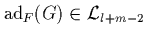 ,
so daß im Spezialfall
,
so daß im Spezialfall 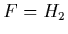 gilt:
gilt:
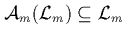 für alle
für alle
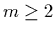 .
Der lineare Operator
.
Der lineare Operator 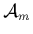 auf dem Vektorraum
auf dem Vektorraum 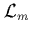 spielt in
der Normalformentheorie für Hamilton-Systeme eine ähnlich bedeutsame
Rolle wie der zu einem linearen Vektorfeld adjungierte Lie-Operator
spielt in
der Normalformentheorie für Hamilton-Systeme eine ähnlich bedeutsame
Rolle wie der zu einem linearen Vektorfeld adjungierte Lie-Operator
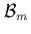 (1.22) in der Normalformentheorie für
Vektorfelder.
(1.22) in der Normalformentheorie für
Vektorfelder.
Um eine Hamilton-Funktion Schritt für Schritt auf ihre -- noch zu
definierende -- Normalform zu transformieren, benötigen wir ein
Gegenstück für die in Abschnitt 1.1.1 verwendete
Transformation (1.16). Hierfür definieren wir den linearen
Operator
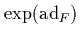 :
:
Definition 1.2
Die
der Potenzreihe
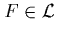
assoziierte Lie-Transformation ist
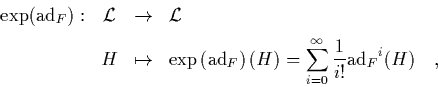 |
(1.36) |
mit
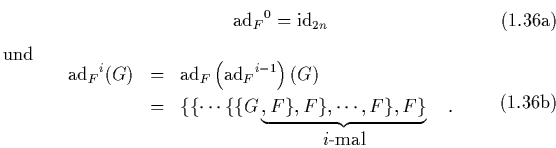
Es wird sich zeigen, daß Transformationen vom Typ (1.48) ein
sehr bequemes und einfach zu handhabendes
Hilfsmittel für die Normalformentheorie darstellen.
Zunächst müssen wir aber sicherstellen, daß die Verwendung von
Lie-Transformationen im Rahmen der Hamilton-Mechanik sinnvoll ist,
insbesondere, daß sie kanonisch sind [De69].
Wir gehen von einem Satz kanonischer Phasenraumkoordinaten
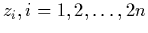 , aus und transformieren diese mittels der
der Potenzreihe
, aus und transformieren diese mittels der
der Potenzreihe 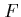 assoziierten Lie-Transformation:
assoziierten Lie-Transformation:
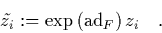 |
(1.36) |
Um die Kanonizität dieser Transformation nachzuweisen, müssen wir
zeigen, daß die fundamentalen Poisson-Klammern
![\begin{displaymath}
\begin{array}{rcl}
\{q_i,p_j\} & = & \delta_{ij} \\ [0.2cm...
...& = & 0 \\ [0.2cm]
\{p_i,p_j\} & = & 0 \\ [0.2cm]
\end{array}\end{displaymath}](img211.png) |
(1.37) |
bzw., mit Gl. (1.46b),
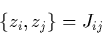 |
(1.38) |
unter (1.50) erhalten bleiben.
Wir untersuchen zunächst allgemein, wie sich Poisson-Klammern unter
Lie-Transformationen verhalten. 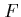 ,
, 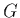 und
und 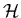 seien aus
seien aus 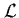 . Dann
gilt, weil für Poisson-Klammern die Jacobi-Identität erfüllt
ist1.5:
. Dann
gilt, weil für Poisson-Klammern die Jacobi-Identität erfüllt
ist1.5:
Mit einer Induktion nach 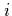 folgt dann
folgt dann
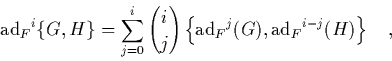 |
(1.40) |
so daß man schließlich für die gesamte Lie-Transformation erhält:
Die Lie-Transformierte der Poisson-Klammer zweier Funktionen ist also
gerade die Poisson-Klammer der Lie-Transformierten dieser Funktionen. Dies
nutzen wir jetzt für den Nachweis der Kanonizität aus. In den neuen,
durch die Transformation (1.50) erhaltenen Variablen
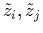 ergeben sich die folgenden Poisson-Klammern:
ergeben sich die folgenden Poisson-Klammern:
Im letzten Schritt haben wir noch ausgenutzt, daß die Poisson-Klammer von
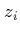 und
und 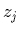 eine Zahl ist (entweder 0 oder 1) und deswegen von
eine Zahl ist (entweder 0 oder 1) und deswegen von
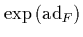 nicht verändert wird.
Gl. (1.56) zeigt die Invarianz der fundamentalen
Poisson-Klammern unter der Lie-Transformation (1.50)
und damit deren
Kanonizität1.6.
nicht verändert wird.
Gl. (1.56) zeigt die Invarianz der fundamentalen
Poisson-Klammern unter der Lie-Transformation (1.50)
und damit deren
Kanonizität1.6.
Um eine anschauliche Interpretation der Lie-Transformation
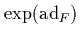 entwickeln zu können, benötigen wir im folgenden die Inverse dieses
Operators. Sie ist auch bei der praktischen Berechnung von
Integralen der Bewegung in Abschnitt 1.2.4 unerläßlich.
Es gilt:
entwickeln zu können, benötigen wir im folgenden die Inverse dieses
Operators. Sie ist auch bei der praktischen Berechnung von
Integralen der Bewegung in Abschnitt 1.2.4 unerläßlich.
Es gilt:
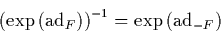 |
(1.43) |
Zum Beweis berechnen wir die Produktabbildung
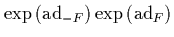 und zeigen, daß sie
gleich der Identität
und zeigen, daß sie
gleich der Identität
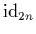 ist. Dabei benutzen wir, daß
ist. Dabei benutzen wir, daß
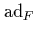 und
und
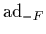 vertauschen:
vertauschen:
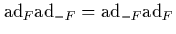 .
.
Mit
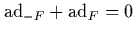 folgt dann die Behauptung.
folgt dann die Behauptung.
Nachdem wir in Gl. (1.56) die Kanonizität der
Lie-Transformation (1.50) gezeigt haben,
beweisen wir jetzt, daß die Hamilton-Funktion 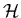 unter einer solchen
kanonischen Transformation in die neue Hamilton-Funktion
unter einer solchen
kanonischen Transformation in die neue Hamilton-Funktion
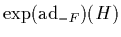 übergeht. Zunächst weisen wir die Beziehung
übergeht. Zunächst weisen wir die Beziehung
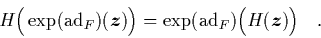 |
(1.44) |
nach. (Auf der linken Seite dieser Gleichung ist mit
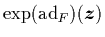 die Anwendung des Operators
die Anwendung des Operators
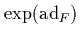 auf jede der Komponenten
auf jede der Komponenten 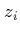 des Vektors
des Vektors
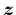 gemeint.) Wir schreiben die linke Seite von Gl. (1.58) als
gemeint.) Wir schreiben die linke Seite von Gl. (1.58) als
und weil
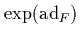 ein linearer Operator ist, gilt für die rechte
Seite der Gleichung:
ein linearer Operator ist, gilt für die rechte
Seite der Gleichung:
Damit bleibt für den Beweis von Gl. (1.58) nur noch zu
zeigen, daß
gilt. Diese Beziehung folgt aber sofort aus
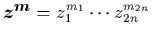 und aus der folgenden
elementaren Eigenschaft einer auf das Produkt zweier Potenzreihen
und aus der folgenden
elementaren Eigenschaft einer auf das Produkt zweier Potenzreihen
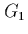 ,
, 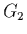 wirkenden Lie-Transformation:
wirkenden Lie-Transformation:
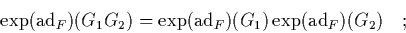 |
(1.45) |
der Beweis dieser Eigenschaft erfolgt völlig
analog zur Herleitung der Beziehung (1.55).
Wir haben damit Gl. (1.58) nachgewiesen und können sie für
die Berechnung der neuen, durch die Lie-Transformation erzeugten
Hamilton-Funktion
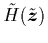 benutzen. Wegen der Gln. (1.50,1.57) ist
benutzen. Wegen der Gln. (1.50,1.57) ist
so daß wir schließlich unter Benutzung von Gl. (1.58) das
erhalten, was zu beweisen war:
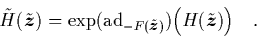 |
(1.46) |
Die Bedeutung von Gl. (1.58) bzw. von Gl. (1.60) liegt darin, daß wir mit ihrer
Hilfe der Lie-Transformation (1.50) eine ganz neue
anschauliche Interpretation geben können:
Wir sehen jetzt in
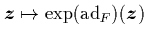 eine
Transformation, die eine Funktion
eine
Transformation, die eine Funktion
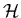 in eine andere Funktion
in eine andere Funktion
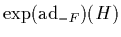 transformiert. Wegen Gl. (1.56) wissen wir, daß diese Transformation kanonisch
ist.
Damit ist die Dynamik des durch die alte Hamilton-Funktion
transformiert. Wegen Gl. (1.56) wissen wir, daß diese Transformation kanonisch
ist.
Damit ist die Dynamik des durch die alte Hamilton-Funktion
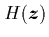 beschriebenen Systems äquivalent zur Dynamik des neuen Hamilton-Systems
beschriebenen Systems äquivalent zur Dynamik des neuen Hamilton-Systems
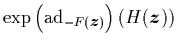 , wenn man beide Systeme
in den
Koordinaten
, wenn man beide Systeme
in den
Koordinaten
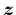 bzw.
bzw.
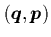 betrachtet. Von diesem
,,aktiven`` Standpunkt aus interpretiert man die Transformation
(1.50) nicht mehr als einen Wechsel der Variablen,
sondern als die Umformung eines Hamilton-Systems in ein anderes, dazu
äquivalentes, wobei das Koordinatensystem unverändert bleibt.
betrachtet. Von diesem
,,aktiven`` Standpunkt aus interpretiert man die Transformation
(1.50) nicht mehr als einen Wechsel der Variablen,
sondern als die Umformung eines Hamilton-Systems in ein anderes, dazu
äquivalentes, wobei das Koordinatensystem unverändert bleibt.
Fußnoten
- ...
Allgemeinheit1.4
- Vgl. hierzu die Fußnote auf Seite
![[*]](crossref.png) .
.
- ...
ist1.5
- Die Tatsache, daß die Poisson-Klammern die
Jacobi-Identität erfüllen, macht
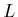 mit der
Produktoperation
mit der
Produktoperation
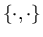 zu einer
Lie-Algebra [Hu87].
zu einer
Lie-Algebra [Hu87].
- ...
Kanonizität1.6
- In [ChEA83] wird ein anderer
Beweis für die Kanonizität von
Lie-Transformationen beschrieben.



Nächste Seite: Die Birkhoff-Gustavson-Normalform
Aufwärts: Normalformen und Quasiintegrale für
Vorherige Seite: Normalformen und Quasiintegrale für
Inhalt
Martin_Engel
2000-05-25
![]() Freiheitsgraden der Bewegung. Die Hamilton-Funktion
Freiheitsgraden der Bewegung. Die Hamilton-Funktion
![]() liege in Form einer formalen Potenzreihe
vor und habe nur Summanden
mit einem (Total-) Grad, der mindestens 2 ist. Wir berücksichtigen also
nur solche Systeme, die einen Fixpunkt haben und legen diesen, ohne
Beschränkung der
Allgemeinheit1.4,
in den Ursprung.
liege in Form einer formalen Potenzreihe
vor und habe nur Summanden
mit einem (Total-) Grad, der mindestens 2 ist. Wir berücksichtigen also
nur solche Systeme, die einen Fixpunkt haben und legen diesen, ohne
Beschränkung der
Allgemeinheit1.4,
in den Ursprung.
![]() -Vektor
-Vektor
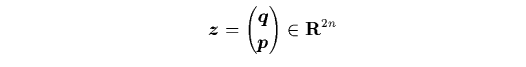
![]()
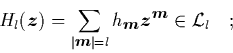
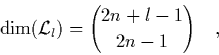
![]() :
:
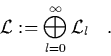
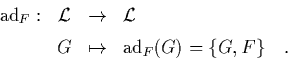
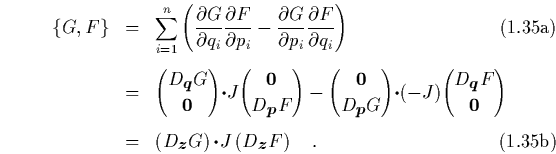
![]() der
Hamilton-Funktion adjungiert ist, setzen wir
der
Hamilton-Funktion adjungiert ist, setzen wir
![]() :
:
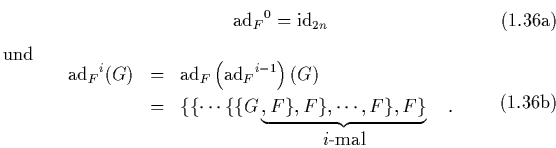
![]() , aus und transformieren diese mittels der
der Potenzreihe
, aus und transformieren diese mittels der
der Potenzreihe ![]() assoziierten Lie-Transformation:
assoziierten Lie-Transformation:
![\begin{displaymath}
\begin{array}{rcl}
\{q_i,p_j\} & = & \delta_{ij} \\ [0.2cm...
...& = & 0 \\ [0.2cm]
\{p_i,p_j\} & = & 0 \\ [0.2cm]
\end{array}\end{displaymath}](img211.png)
![]() ,
, ![]() und
und ![]() seien aus
seien aus ![]() . Dann
gilt, weil für Poisson-Klammern die Jacobi-Identität erfüllt
ist1.5:
. Dann
gilt, weil für Poisson-Klammern die Jacobi-Identität erfüllt
ist1.5:
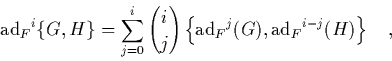
![]() entwickeln zu können, benötigen wir im folgenden die Inverse dieses
Operators. Sie ist auch bei der praktischen Berechnung von
Integralen der Bewegung in Abschnitt 1.2.4 unerläßlich.
Es gilt:
entwickeln zu können, benötigen wir im folgenden die Inverse dieses
Operators. Sie ist auch bei der praktischen Berechnung von
Integralen der Bewegung in Abschnitt 1.2.4 unerläßlich.
Es gilt:
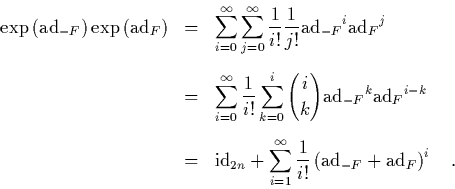
![]() unter einer solchen
kanonischen Transformation in die neue Hamilton-Funktion
unter einer solchen
kanonischen Transformation in die neue Hamilton-Funktion
![]() übergeht. Zunächst weisen wir die Beziehung
übergeht. Zunächst weisen wir die Beziehung
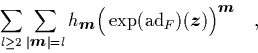
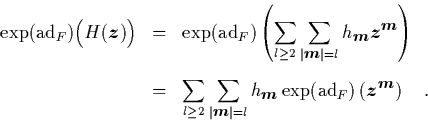
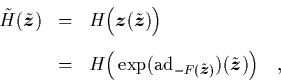
![]() eine
Transformation, die eine Funktion
eine
Transformation, die eine Funktion
![]() in eine andere Funktion
in eine andere Funktion
![]() transformiert. Wegen Gl. (1.56) wissen wir, daß diese Transformation kanonisch
ist.
Damit ist die Dynamik des durch die alte Hamilton-Funktion
transformiert. Wegen Gl. (1.56) wissen wir, daß diese Transformation kanonisch
ist.
Damit ist die Dynamik des durch die alte Hamilton-Funktion
![]() beschriebenen Systems äquivalent zur Dynamik des neuen Hamilton-Systems
beschriebenen Systems äquivalent zur Dynamik des neuen Hamilton-Systems
![]() , wenn man beide Systeme
in den
Koordinaten
, wenn man beide Systeme
in den
Koordinaten
![]() bzw.
bzw.
![]() betrachtet. Von diesem
,,aktiven`` Standpunkt aus interpretiert man die Transformation
(1.50) nicht mehr als einen Wechsel der Variablen,
sondern als die Umformung eines Hamilton-Systems in ein anderes, dazu
äquivalentes, wobei das Koordinatensystem unverändert bleibt.
betrachtet. Von diesem
,,aktiven`` Standpunkt aus interpretiert man die Transformation
(1.50) nicht mehr als einen Wechsel der Variablen,
sondern als die Umformung eines Hamilton-Systems in ein anderes, dazu
äquivalentes, wobei das Koordinatensystem unverändert bleibt.
![[*]](crossref.png) .
.