



Next: Localized Wave Packets in
Up: ANDERSON Localization in the
Previous: ANDERSON Localization on One-dimensional
Contents
Mapping of the Quantum Kicked Rotor onto the
ANDERSON Model
Combining the results of the two preceding subsections,
I now present the argument showing
that the quantum kicked rotor exhibits ANDERSON localization,
by deriving a mapping of the rotor
model
onto the ANDERSON model
[FGP82,GFP82,PGF83].
I begin this discussion of the quantum map (5.8)
with
a general kick potential 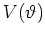 ,
,
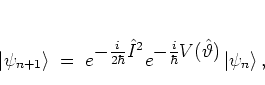 |
(5.31) |
and specialize to particular potentials -- the cosine potential
(5.2) being one of two to be considered --
later in the course of the discussion.
Using the results of subsection 2.1.1,
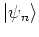 can be expanded in terms of the quasienergy states of the kicked rotor
can be expanded in terms of the quasienergy states of the kicked rotor
 with constant coefficients
with constant coefficients 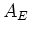 :
:
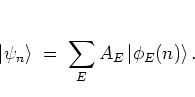 |
(5.32) |
Since the
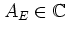 are time-independent
it suffices to consider in the
following the time evolution of a single quasienergy state
rather than the general
are time-independent
it suffices to consider in the
following the time evolution of a single quasienergy state
rather than the general
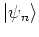 of equation
(5.44).
of equation
(5.44).
For the investigation of the kicked rotor the states
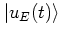 are much better suited than the full quasienergy states
are much better suited than the full quasienergy states
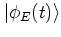 ,
since by the periodicity (2.24) the time
argument can be dropped altogether. This allows to map
the dynamical system
(5.43) onto a static problem.
In accordance with the discrete nature of the kick, I define the
(reduced) quasienergy states immediately before and after the kicks as
,
since by the periodicity (2.24) the time
argument can be dropped altogether. This allows to map
the dynamical system
(5.43) onto a static problem.
In accordance with the discrete nature of the kick, I define the
(reduced) quasienergy states immediately before and after the kicks as
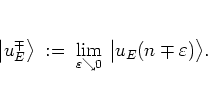 |
(5.33) |
In terms of the new states the quantum map can now be formulated as
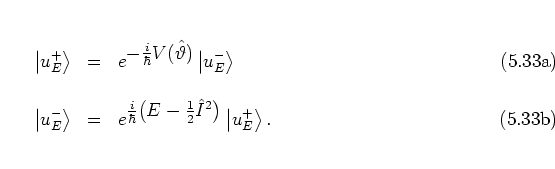
It turns out that the kick part (5.46a) of the dynamics is
most conveniently described using the averaged state
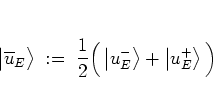 |
(5.33) |
and
exchanging
the potential
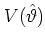 for
the
expression
for
the
expression
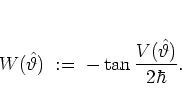 |
(5.34) |
This definition of
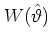 can be used to rewrite the kick propagator as
can be used to rewrite the kick propagator as
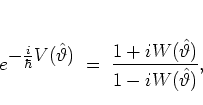 |
(5.35) |
such that I obtain by
substitution
into equation (5.46a):
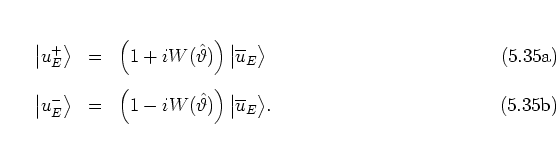
Inserting
these expressions into the equation (5.46b)
that describes
the free part of the dynamics, the
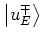 are
eliminated from the equation and the dynamics is entirely formulated in
terms of the averaged quasienergy state
are
eliminated from the equation and the dynamics is entirely formulated in
terms of the averaged quasienergy state
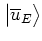 :
:
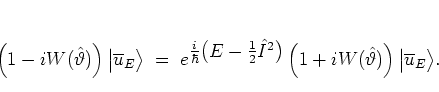 |
(5.35) |
In order to facilitate the evaluation of the action of the angular
momentum operator 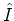 , this equation is projected onto the
eigenstates
, this equation is projected onto the
eigenstates
 of
of 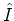 (see equation (5.12)). To this end
I define
(see equation (5.12)). To this end
I define
![\begin{displaymath}
\overline{u}_{E,m}
\; := \; \rule[-0.1cm]{0.0cm}{0.1cm}_{\...
...left\vert \overline{u}_E \right> \right., \quad m\in\mathbb{Z}
\end{displaymath}](img1031.png) |
(5.36) |
and obtain
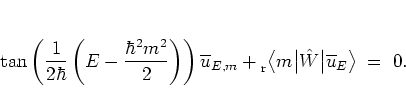 |
(5.37) |
It remains to evaluate the matrix element
![$\rule[-0.1cm]{0.0cm}{0.1cm}_{\rm r} \big< m \big\vert \hat{W} \big\vert \overline{u}_E \big>$](img1033.png) .
By virtue of the representation (5.12) of
.
By virtue of the representation (5.12) of
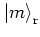 it is easily seen that the matrix element
it is easily seen that the matrix element
![$\rule[-0.1cm]{0.0cm}{0.1cm}_{\rm r} \big< m \big\vert \hat{W} \big\vert m' \big>_{\rm r}$](img1034.png) satisfies
satisfies
![\begin{displaymath}
\rule[-0.1cm]{0.0cm}{0.1cm}_{\rm r} \big< m \big\vert \hat{...
...hat{W} \big\vert 0 \big>_{\rm r}
\; ,
\quad m'\in\mathbb{Z},
\end{displaymath}](img1035.png) |
(5.38) |
i.e. the matrix element depends on the difference of the quantum numbers
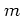 ,
, 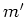 only.
Therefore it makes sense to use just a single index
only.
Therefore it makes sense to use just a single index 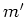 and define
the ``interaction energy''
as5.7
and define
the ``interaction energy''
as5.7
![\begin{displaymath}
W_{m'} \; := \; % \frac{1}{\sqrt{2\pi}} \,
\rule[-0.1cm]{0...
...rt \hat{W} \big\vert 0 \big>_{\rm r},
% \; , \quad m'\in\ZZ,
\end{displaymath}](img1037.png) |
(5.39) |
in terms of which the matrix element
![$\rule[-0.1cm]{0.0cm}{0.1cm}_{\rm r} \big< m \big\vert \hat{W} \big\vert \overline{u}_E \big>$](img1033.png) reads:
reads:
![\begin{displaymath}
\rule[-0.1cm]{0.0cm}{0.1cm}_{\rm r}
\big< m \big\vert \hat...
...sum_{m'=-\infty}^\infty \, W_{m'} \, \overline{u}_{E,m-m'}\; .
\end{displaymath}](img1038.png) |
(5.40) |
In the end one thus arrives at an equation analogous to the discrete
SCHRÖDINGER equation (5.20) with 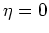 ,
,
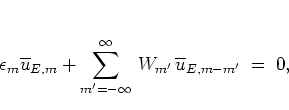 |
(5.41) |
with the diagonal energies
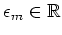 given by
given by
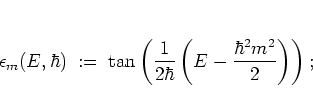 |
(5.42) |
the hopping matrix elements 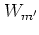 describe the
coupling
of a ``site of the lattice''
describe the
coupling
of a ``site of the lattice''
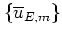 with its
with its 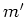 -th nearest neighbour,
due to the kick. By the property (5.54) this
coupling depends on the distance between the two sites only, which means
that the
system is translation invariant.
-th nearest neighbour,
due to the kick. By the property (5.54) this
coupling depends on the distance between the two sites only, which means
that the
system is translation invariant.
Note that in general
equation (5.57)
is not
a tight binding equation
(5.31), since the interaction is not restricted to just the
respective nearest neighbours of each site.
In fact, the cosine potential (5.2) leads to
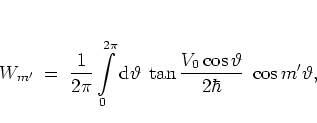 |
(5.43) |
which implies that 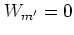 for even
for even 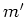 , but also that,
generally speaking, all
, but also that,
generally speaking, all 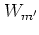 for odd
for odd 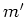 are possibly nonzero.
Nevertheless, for this cosine potential
are possibly nonzero.
Nevertheless, for this cosine potential 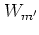 decays rapidly
-- obviously exponentially -- with
decays rapidly
-- obviously exponentially -- with
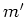 , as figure 5.7 shows, where
, as figure 5.7 shows, where 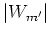 (obtained by numerical evaluation of the integral in equation
(5.59),
since a closed formula for this integral is lacking)
as a function of
(obtained by numerical evaluation of the integral in equation
(5.59),
since a closed formula for this integral is lacking)
as a function of 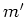 is plotted for several parameter combinations.
The figure
indicates that the corresponding discrete SCHRÖDINGER equation
(5.57), while not exactly describing a
tight binding model, is a good approximation to a tight binding equation
for suitable combinations of the parameters
is plotted for several parameter combinations.
The figure
indicates that the corresponding discrete SCHRÖDINGER equation
(5.57), while not exactly describing a
tight binding model, is a good approximation to a tight binding equation
for suitable combinations of the parameters  ,
, 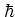 .
Namely, equation (5.57) becomes a true
tight binding equation in the limit
.
Namely, equation (5.57) becomes a true
tight binding equation in the limit
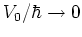 , i.e. for weak
perturbations
and/or in the fully quantum mechanical regime specified by large values
of
, i.e. for weak
perturbations
and/or in the fully quantum mechanical regime specified by large values
of 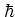 .
The tight binding system
.
The tight binding system
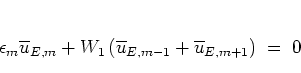 |
(5.44) |
obtained in this limit can be described
-- in analogy to the transfer matrix
(5.33) in ANDERSON's theory
--
by the transfer matrix5.8
![\begin{displaymath}
\cal{T}_m
\; = \; \left( \begin{array}{cc}
\displaystyle ...
...silon_m}{W_1}\;\; & -1 \\ [0.5cm]
1 & 0
\end{array} \right),
\end{displaymath}](img1050.png) |
(5.45) |
acting on the vectors
![\begin{subequations}
\begin{eqnarray}
\vec{u}_{E,m} & := & { \overline{u}_{E,m}...
...verline{u}_{E,m} }
\rule[-0.7cm]{0.0cm}{0.7cm}
\end{eqnarray}\end{subequations}](img1051.png)
via

-- cf. the vectors
(5.32, 5.36)
and the
``equations of motion''
(5.34, 5.37)
of the ANDERSON model in subsection 5.1.2.
By choosing a different kick potential 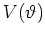 the transition to a
true tight binding model may be achieved. The choice of the potential
affects the hopping matrix elements only and leaves the diagonal energies
unchanged. For the alternate potential
the transition to a
true tight binding model may be achieved. The choice of the potential
affects the hopping matrix elements only and leaves the diagonal energies
unchanged. For the alternate potential
 |
(5.44) |
with
arbitrary real constants 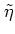 and
and
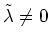 ,
the corresponding alternate hopping matrix elements are
,
the corresponding alternate hopping matrix elements are
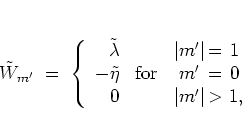 |
(5.45) |
such that with this
potential one
gets a tight binding
model
without having to rely on an approximation:
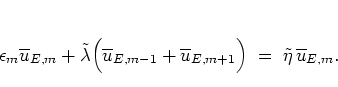 |
(5.46) |
For
all
practical purposes the diagonal energies 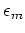 of
(5.58)
can be taken to be randomly distributed as in the
ANDERSON-LLOYD model, which can be seen as follows.
In the absence of the
quantum resonances [Fis93]
defined by
of
(5.58)
can be taken to be randomly distributed as in the
ANDERSON-LLOYD model, which can be seen as follows.
In the absence of the
quantum resonances [Fis93]
defined by
 |
(5.47) |
the
argument
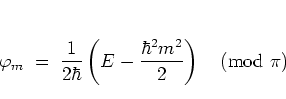 |
(5.48) |
of the tangent
in equation (5.58) is
pseudo- or
quasi-random5.9and uniformly distributed
in the interval
![$[-\pi/2,\pi/2]$](img1061.png) .
This
implies that the corresponding distribution function
.
This
implies that the corresponding distribution function 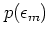 for the diagonal energies satisfies
for the diagonal energies satisfies
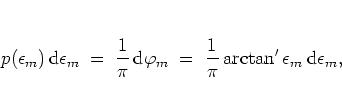 |
(5.49) |
and therefore
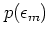 turns out to be
a Lorentzian (with
turns out to be
a Lorentzian (with 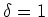 in terms of equation (5.41)):
in terms of equation (5.41)):
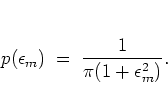 |
(5.50) |
Figure 5.8a confirms this
generic
distribution of the
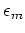 in the case of
in the case of 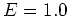 and
and 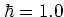 .
Figure 5.8b, on the other hand, shows
the distribution of the
.
Figure 5.8b, on the other hand, shows
the distribution of the 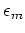 for the just slightly detuned value
for the just slightly detuned value
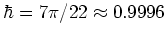 ;
in this particular example of quantum resonance,
due to the implicit modulo operation in equation (5.58)
;
in this particular example of quantum resonance,
due to the implicit modulo operation in equation (5.58)
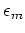 takes on only 18 different values,
as opposed to the continuous range of values
obtained for
takes on only 18 different values,
as opposed to the continuous range of values
obtained for 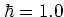 . Thus it may be claimed that for resonant values
of
. Thus it may be claimed that for resonant values
of 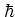 the resulting
the resulting 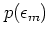 is not well-behaved enough
(e.g. not smooth enough) for FURSTENBERG's theorem to apply.
This interpretation is in agreement with the well-known fact that in the
resonant case the quantum states typically (but not always) are
delocalized [Fis93].
For nonresonant
is not well-behaved enough
(e.g. not smooth enough) for FURSTENBERG's theorem to apply.
This interpretation is in agreement with the well-known fact that in the
resonant case the quantum states typically (but not always) are
delocalized [Fis93].
For nonresonant 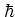 , and thus for a Lorentzian quasi-random
distribution of the diagonal energies, it can be shown
(see equation (B.6) in appendix
B) that FURSTENBERG's integrability condition
(B.2) is satisfied.
, and thus for a Lorentzian quasi-random
distribution of the diagonal energies, it can be shown
(see equation (B.6) in appendix
B) that FURSTENBERG's integrability condition
(B.2) is satisfied.
For the above reasoning the presence of the additional factor 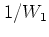 in
the matrix element
in
the matrix element
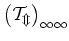 of equation (5.61)
(as compared with equation (5.33)) is irrelevant:
the condition (B.2) is satisfied for the
matrix (5.61) if and only if it is satisfied for
the matrix (5.33).
of equation (5.61)
(as compared with equation (5.33)) is irrelevant:
the condition (B.2) is satisfied for the
matrix (5.61) if and only if it is satisfied for
the matrix (5.33).
Note that the quantum resonances (5.67) are an
entirely quantum mechanical phenomenon
that does not have a classical
counterpart. In this respect the quantum resonances of the
kicked rotor are similar to the quantum resonances
(4.7, 4.44, 4.49) of the
resonant (with respect to 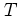 )
kicked harmonic oscillator discussed in subsections
4.1.2 and 4.2.2.
The resonances (1.23/4.22)
with respect to
)
kicked harmonic oscillator discussed in subsections
4.1.2 and 4.2.2.
The resonances (1.23/4.22)
with respect to 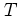 , on the other hand, can also
be viewed as a truly quantum mechanical phenomenon, but nevertheless
they play an important role classically, too.
, on the other hand, can also
be viewed as a truly quantum mechanical phenomenon, but nevertheless
they play an important role classically, too.
Putting all the above pieces together, a mapping from the quantum kicked
rotor
in the case of quantum nonresonance
onto the ANDERSON-LLOYD model
--
defined by equations
(5.33, 5.34, 5.41)
--
has been established, and
the results on
ANDERSON localization reviewed in the previous subsection carry
over
to the rotor. Using the same genericity assumptions as in subsection
5.1.2
(see pages ![[*]](crossref.png) f),
the averaged time-independent quasienergy
states
f),
the averaged time-independent quasienergy
states
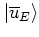 are found to be exponentially
localized
with respect to rotor (angular momentum) eigenstates;
the localization length
are found to be exponentially
localized
with respect to rotor (angular momentum) eigenstates;
the localization length
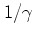 can be derived along the same lines as equation (5.42)
for
can be derived along the same lines as equation (5.42)
for 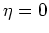 ,
, 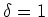 :
:
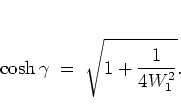 |
(5.51) |
This in turn means that every
generic sequence of states
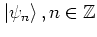 , generated by the
quantum map (5.43) consists of localized states.
In other words: the quantum kicked rotor is ANDERSON-localized.
Consequences of this type of localization of quantum states are discussed
below in
sections 5.2 and 5.3
with respect to similarly localized
states of the quantum kicked harmonic oscillator.
, generated by the
quantum map (5.43) consists of localized states.
In other words: the quantum kicked rotor is ANDERSON-localized.
Consequences of this type of localization of quantum states are discussed
below in
sections 5.2 and 5.3
with respect to similarly localized
states of the quantum kicked harmonic oscillator.
It is interesting to note the different roles the parameters  and
and
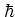 play with respect to the details of the localization mechanism.
Regardless of the value of
play with respect to the details of the localization mechanism.
Regardless of the value of  ,
the (resonant or nonresonant) value of
,
the (resonant or nonresonant) value of 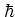 alone decides
on the existence of localization.
alone decides
on the existence of localization.
 , on the other hand,
divided by
, on the other hand,
divided by
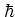 controls the localization length via equations
(5.59) and (5.71).
controls the localization length via equations
(5.59) and (5.71).
While by the above arguments it has been shown that there exists a
very
close relationship between the quantum kicked rotor and the ANDERSON model, it has to be stressed that until now no
mathematically rigorous
proof
has been found for exact equivalence of
both
model systems [CIS98], one of the reasons
being
that a tight binding equation for the rotor is obtained as an
-- albeit good --
approximation only;
in addition, the
consequences
of the quantum resonances (5.67)
for
such a potential proof are not yet
completely understood.
The ongoing effort to establish a complete analogy between the
quantum kicked rotor and an ANDERSON-like model is documented in
[AZ96,CIS98,AZ98],
for example.
The lack of mathematically rigorous equivalence may also be expressed by
noting that the
sample
kick potential (5.64), which
leads to the tight binding equation (5.66), differs
from the original kick potential (5.2).
Nevertheless, this explanation of localization in the quantum kicked rotor
is generally accepted, and all available numerical evidence supports the
equivalence of the two model systems, as far as localization is concerned
[Haa01].
In this way the numerical findings of subsection 5.1.1,
especially the results on saturation of energy growth of the quantum
kicked rotor displayed in figure 5.4, find a
satisfactory explanation.
Footnotes
- ...
as5.7
- In general,
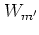 does not take on real values only.
However, for kick potentials
does not take on real values only.
However, for kick potentials 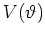 that are even with
respect to
that are even with
respect to 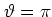 ,
, 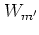 is real, thus justifying
the characterization as an energy. The potential
(5.2) falls into this category.
is real, thus justifying
the characterization as an energy. The potential
(5.2) falls into this category.
- ... matrix5.8
- Without loss of generality
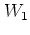 can be assumed to be
nonzero
-- this assumption is identical with assuming nontriviality of the
tight-binding equation (5.60) --
such that
dividing
by
can be assumed to be
nonzero
-- this assumption is identical with assuming nontriviality of the
tight-binding equation (5.60) --
such that
dividing
by 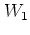 is not a problem: for the construction of the
appropriate tight binding system it suffices to consider the first
nonvanishing matrix element
is not a problem: for the construction of the
appropriate tight binding system it suffices to consider the first
nonvanishing matrix element 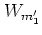 .
A sample tight binding equation with
.
A sample tight binding equation with 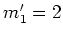 is given below
in equation (5.101).
(But note that that equation is for the kicked harmonic oscillator
rather than the kicked rotor; this accounts for some differences in
details which are discussed there.)
is given below
in equation (5.101).
(But note that that equation is for the kicked harmonic oscillator
rather than the kicked rotor; this accounts for some differences in
details which are discussed there.)
- ...
quasi-random5.9
- In the case of quantum-nonresonance in the sense of equation
(5.67),
despite the deterministic quadratic dependence on
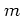 ,
,
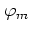 effectively becomes
randomly distributed in the interval
effectively becomes
randomly distributed in the interval
![$[-\pi/2,\pi/2]$](img1061.png) by the implicit modulo operation, due to the
periodicity of the tangent
in equation (5.58).
by the implicit modulo operation, due to the
periodicity of the tangent
in equation (5.58).




Next: Localized Wave Packets in
Up: ANDERSON Localization in the
Previous: ANDERSON Localization on One-dimensional
Contents
Martin Engel 2004-01-01
![]() ,
,
![]() are much better suited than the full quasienergy states
are much better suited than the full quasienergy states
![]() ,
since by the periodicity (2.24) the time
argument can be dropped altogether. This allows to map
the dynamical system
(5.43) onto a static problem.
In accordance with the discrete nature of the kick, I define the
(reduced) quasienergy states immediately before and after the kicks as
,
since by the periodicity (2.24) the time
argument can be dropped altogether. This allows to map
the dynamical system
(5.43) onto a static problem.
In accordance with the discrete nature of the kick, I define the
(reduced) quasienergy states immediately before and after the kicks as
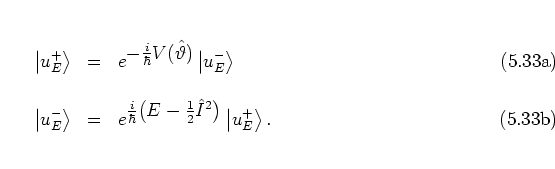
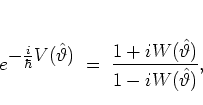
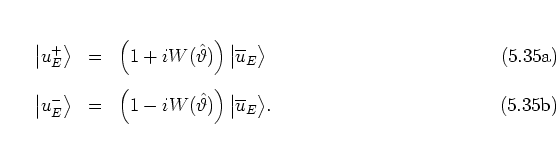
![]() are
eliminated from the equation and the dynamics is entirely formulated in
terms of the averaged quasienergy state
are
eliminated from the equation and the dynamics is entirely formulated in
terms of the averaged quasienergy state
![]() :
:
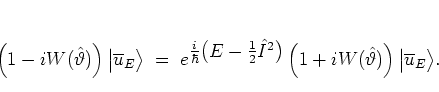
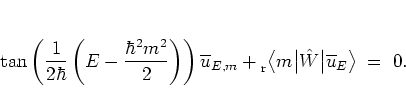
![]() .
By virtue of the representation (5.12) of
.
By virtue of the representation (5.12) of
![]() it is easily seen that the matrix element
it is easily seen that the matrix element
![]() satisfies
satisfies
![\begin{displaymath}
W_{m'} \; := \; % \frac{1}{\sqrt{2\pi}} \,
\rule[-0.1cm]{0...
...rt \hat{W} \big\vert 0 \big>_{\rm r},
% \; , \quad m'\in\ZZ,
\end{displaymath}](img1037.png)
![\begin{displaymath}
\rule[-0.1cm]{0.0cm}{0.1cm}_{\rm r}
\big< m \big\vert \hat...
...sum_{m'=-\infty}^\infty \, W_{m'} \, \overline{u}_{E,m-m'}\; .
\end{displaymath}](img1038.png)
![]() ,
,
![\begin{subequations}
\begin{eqnarray}
\vec{u}_{E,m} & := & { \overline{u}_{E,m}...
...verline{u}_{E,m} }
\rule[-0.7cm]{0.0cm}{0.7cm}
\end{eqnarray}\end{subequations}](img1051.png)

![]() the transition to a
true tight binding model may be achieved. The choice of the potential
affects the hopping matrix elements only and leaves the diagonal energies
unchanged. For the alternate potential
the transition to a
true tight binding model may be achieved. The choice of the potential
affects the hopping matrix elements only and leaves the diagonal energies
unchanged. For the alternate potential
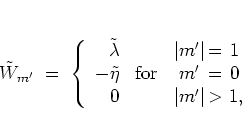
![]() of
(5.58)
can be taken to be randomly distributed as in the
ANDERSON-LLOYD model, which can be seen as follows.
In the absence of the
quantum resonances [Fis93]
defined by
of
(5.58)
can be taken to be randomly distributed as in the
ANDERSON-LLOYD model, which can be seen as follows.
In the absence of the
quantum resonances [Fis93]
defined by
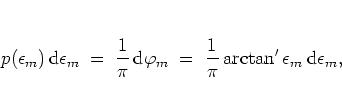
![]() in
the matrix element
in
the matrix element
![]() of equation (5.61)
(as compared with equation (5.33)) is irrelevant:
the condition (B.2) is satisfied for the
matrix (5.61) if and only if it is satisfied for
the matrix (5.33).
of equation (5.61)
(as compared with equation (5.33)) is irrelevant:
the condition (B.2) is satisfied for the
matrix (5.61) if and only if it is satisfied for
the matrix (5.33).
![]() )
kicked harmonic oscillator discussed in subsections
4.1.2 and 4.2.2.
The resonances (1.23/4.22)
with respect to
)
kicked harmonic oscillator discussed in subsections
4.1.2 and 4.2.2.
The resonances (1.23/4.22)
with respect to ![]() , on the other hand, can also
be viewed as a truly quantum mechanical phenomenon, but nevertheless
they play an important role classically, too.
, on the other hand, can also
be viewed as a truly quantum mechanical phenomenon, but nevertheless
they play an important role classically, too.
![[*]](crossref.png) f),
the averaged time-independent quasienergy
states
f),
the averaged time-independent quasienergy
states
![]() are found to be exponentially
localized
with respect to rotor (angular momentum) eigenstates;
the localization length
are found to be exponentially
localized
with respect to rotor (angular momentum) eigenstates;
the localization length
![]() can be derived along the same lines as equation (5.42)
for
can be derived along the same lines as equation (5.42)
for ![]() ,
, ![]() :
:
![]() and
and
![]() play with respect to the details of the localization mechanism.
Regardless of the value of
play with respect to the details of the localization mechanism.
Regardless of the value of ![]() ,
the (resonant or nonresonant) value of
,
the (resonant or nonresonant) value of ![]() alone decides
on the existence of localization.
alone decides
on the existence of localization.
![]() , on the other hand,
divided by
, on the other hand,
divided by
![]() controls the localization length via equations
(5.59) and (5.71).
controls the localization length via equations
(5.59) and (5.71).